



Next: 11.3 Alternating Series
Up: 11. Infinite Series
Previous: 11.1 Infinite Series
Index
In this section we prove a number of theorems about convergence of series of real
numbers. Later we will show how to use these results to study convergence of complex
sequences.
11.11
Theorem (Comparison test for series.)
Let 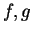 be two sequences of non-negative numbers. Suppose that there is a number
be two sequences of non-negative numbers. Suppose that there is a number
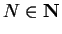 such that
Then
and
such that
Then
and
Proof: Note that the two statements in the conclusion are equivalent, so it is
sufficient to prove the first.
Suppose that  is summable. Then
is summable. Then 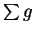 converges, so
converges, so 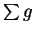 is bounded --
say
is bounded --
say
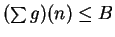 for all
for all
 . Then
for all
. Then
for all 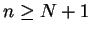 ,
,
Since for 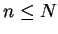 we have
we have
we see that 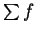 is bounded by
is bounded by
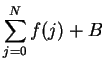 . Also
. Also 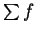 is
increasing, since
is
increasing, since
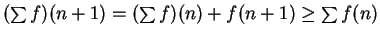 . Hence
. Hence 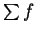 is
bounded and increasing, and hence
is
bounded and increasing, and hence 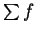 converges; i.e.,
converges; i.e.,  is summable.
is summable.

11.12
Examples.
Since
and
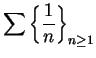
diverges, it follows that
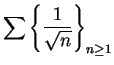
also diverges. Since
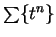
converges for
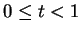
,
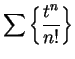
also converges for
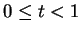
.
In order to use the comparison test, we need to have some standard series to compare
other series with. The next theorem will provide a large family of standard series.
11.13
Theorem.
Let
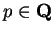 . Then
. Then
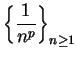 is summable if
is summable if 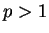 , and
is not summable if
, and
is not summable if 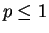 .
.
Proof: Let
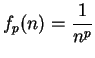 for
for
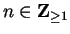 . Then for all
. Then for all
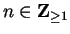 and all
and all 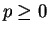 ,
,
Hence,
If 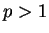 , then
, then 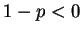 , so
, so 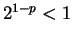 and
and 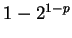 is positive. Hence
is positive. Hence
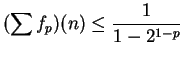 ; i.e., the sequence
; i.e., the sequence 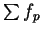 is bounded. It is
also increasing, so it converges.
is bounded. It is
also increasing, so it converges.
If 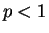 , then
, then
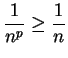 , so by using the comparison test
with the harmonic series,
, so by using the comparison test
with the harmonic series, 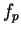 is not summable.
is not summable.

11.14
Remark.
For
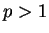
, the proof of the previous theorem shows that
Hence, we get
and
The exact values of the series (found by Euler) are
and
11.15
Examples.
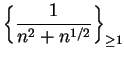
is summable, since
and
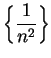
is summable.
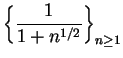 is not summable since
is not summable since
and
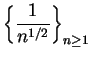
is not summable.
11.16
Example.
Let
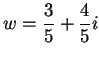
, and let
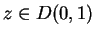
. Then
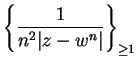
is summable.
Proof: By the reverse triangle inequality, we have for all
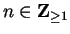
so
Since
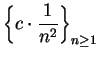 is a summable sequence for
all
is a summable sequence for
all
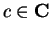 , it follows from the comparison test that
, it follows from the comparison test that
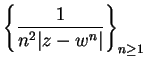 is summable.
is summable.

11.17
Example.
Let
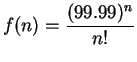
for all

. Then
If
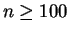
, then
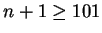
, so
Hence,
Hence, (by induction)
where
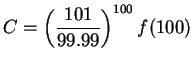
; i.e.,
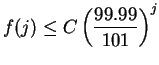
for all
. Since the geometric series
converges, it
follows from the comparison test that
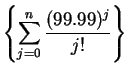
converges also.
11.20
Theorem (Limit comparison test.)
Let 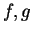 be sequences of positive numbers. Suppose that
be sequences of positive numbers. Suppose that
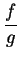 converges
to a non-zero limit
converges
to a non-zero limit 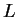 . Then
. Then  is summable if and only if
is summable if and only if 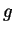 is summable.
is summable.
Proof: We know that 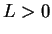 . Let
. Let
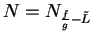 be a precision
function for
be a precision
function for
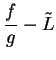 . Then
. Then
i.e.,
If 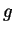 is summable, then
is summable, then
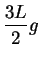 is summable, and since
is summable, and since
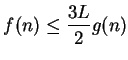 for all
for all
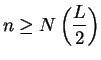 , it follows
from the comparison test that
, it follows
from the comparison test that  is summable. If
is summable. If 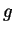 is not summable,
then since
is not summable,
then since
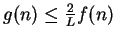 for all
for all
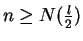 it follows
that
it follows
that
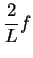 is not summable, and hence
is not summable, and hence  is not summable.
is not summable.

11.21
Example.
Is
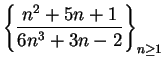
summable? Let
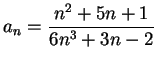
. Note that
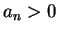
for all
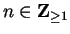
. For large
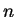
,
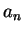
is `` like"
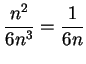
, so I'll compare this series with
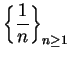
. Let
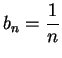
for all
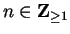
. Then
so
Since
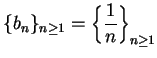
is not summable,
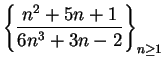
is also not summable.
11.22
Exercise.
Determine whether or not the sequences below are summable.
- a)
-
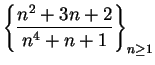 .
.
- b)
-
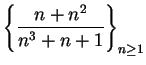 .
.
11.23
Theorem (Ratio test.)
Let 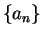 be a sequence of positive numbers. Suppose the
be a sequence of positive numbers. Suppose the
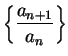 converges, and
converges, and
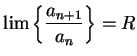 . Then, if
. Then, if 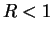 ,
, 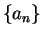 is summable. If
is summable. If 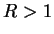 ,
, 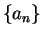 is
not summable. (If
is
not summable. (If 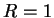 , the theorem makes no assertion.)
, the theorem makes no assertion.)
Proof: Suppose
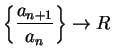 .
.
- Case 1:
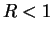 . Let
. Let 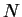 be a precision function for
be a precision function for
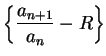 . Then for all
. Then for all
 ,
,
Write
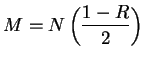 and
and
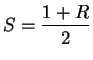 , so
, so
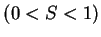 . Then
. Then
so
and (by an induction argument which I omit)
or
or
Since 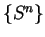 is a summable geometric series, it follows from the comparison test
that
is a summable geometric series, it follows from the comparison test
that 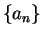 is also summable.
is also summable.
- Case 2:
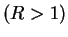 . As before, let
. As before, let 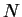 be a precision function for
be a precision function for
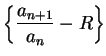 . Then for all
. Then for all
 ,
,
Hence 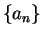 is not a null sequence. So
is not a null sequence. So 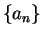 is not summable.
is not summable.

11.25
Remark.
If, in applying the ratio test, you find that
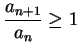
for all large
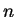
, you can conclude that
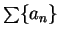
diverges (even if
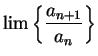
does not exist), since this
condition shows that
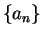
is not a null sequence.
11.26
Example.
Let
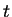
be a positive number and let
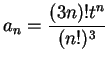
. We apply
the ratio test to the series
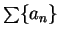
.
Note that
Hence
From this we see that
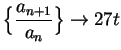
. The ratio test says that if
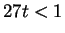
(i.e., if
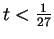
), then
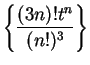
is summable, and
if
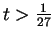
, then the sequence is not summable.
Can we figure out what happens in the case
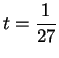 ? For
? For
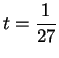 , our formula above gives us
, our formula above gives us
i.e.,
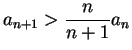
for
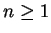
. Thus,
and (by induction),
Since
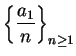
is not summable, it follows
that
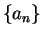
is not summable for
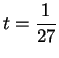
.
11.27
Example.
Let
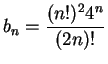
for all

. I'll apply
ratio test to
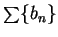
. For all

,
Hence
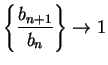
and the ratio test does not
apply. But since
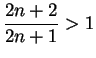
for all
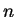
, I conclude that
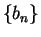
is an increasing sequence and hence
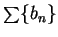
diverges.




Next: 11.3 Alternating Series
Up: 11. Infinite Series
Previous: 11.1 Infinite Series
Index
![]() is summable. Then
is summable. Then ![]() converges, so
converges, so ![]() is bounded --
say
is bounded --
say
![]() for all
for all
![]() . Then
for all
. Then
for all ![]() ,
,
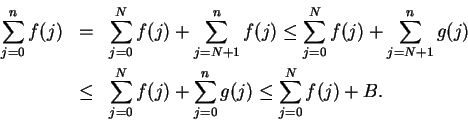
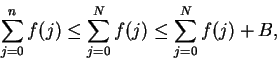
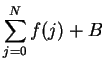 . Also
. Also 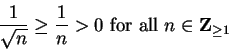
 diverges, it follows that
diverges, it follows that
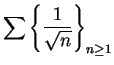 also diverges. Since
also diverges. Since
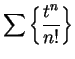 also converges for
also converges for 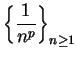 is summable if
is summable if 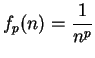 for
for
![]() . Then for all
. Then for all
![]() and all
and all ![]() ,
,
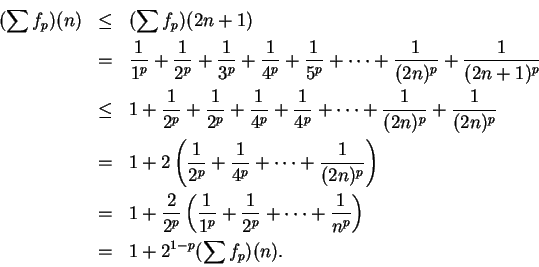
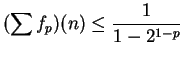 ; i.e., the sequence
; i.e., the sequence ![]() , then
, then
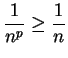 , so by using the comparison test
with the harmonic series,
, so by using the comparison test
with the harmonic series, ![]() is not summable.
is not summable.
![]()
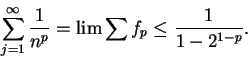
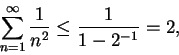
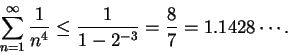
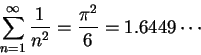
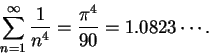
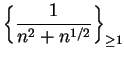 is summable, since
is summable, since
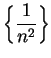 is summable.
is summable.
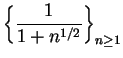 is not summable since
is not summable since
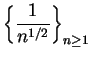 is not summable.
is not summable.
 , and let
, and let 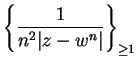 is summable.
is summable.
![]()
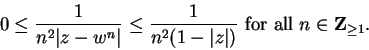
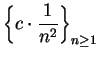 is a summable sequence for
all
is a summable sequence for
all
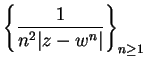 is summable.
is summable.
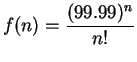 for all
for all
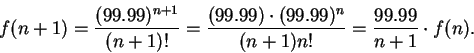
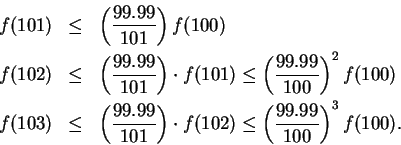
![\begin{eqnarray*}
f(100+n)&\leq&\left({{99.99}\over {101}}\right)^n f(100)\\
&=...
...}f(100)\right] \\
&=&C\left({{99.99}\over {101}}\right)^{100+n}
\end{eqnarray*}](img1435.gif)
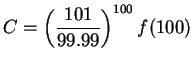 ; i.e.,
; i.e.,
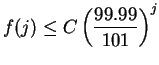 for all
for all 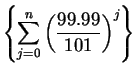 converges, it
follows from the comparison test that
converges, it
follows from the comparison test that
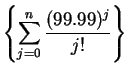 converges also.
converges also.
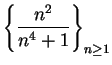
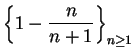
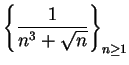
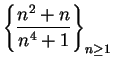
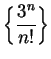
![]() . Let
. Let
![]() be a precision
function for
be a precision
function for
 . Then
. Then
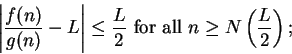
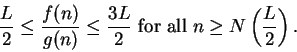
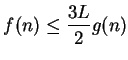 for all
for all
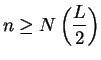 , it follows
from the comparison test that
, it follows
from the comparison test that 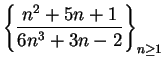 summable? Let
summable? Let
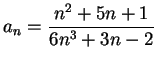 . Note that
. Note that 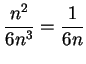 , so I'll compare this series with
, so I'll compare this series with
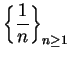 . Let
. Let
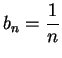 for all
for all
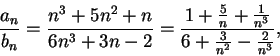
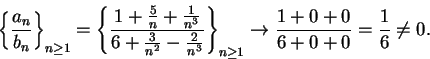
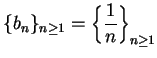 is not summable,
is not summable,
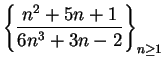 is also not summable.
is also not summable.
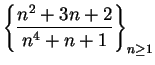 .
.
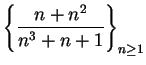 .
.
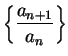 converges, and
converges, and
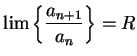 . Then, if
. Then, if 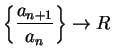 .
.
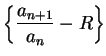 . Then for all
. Then for all
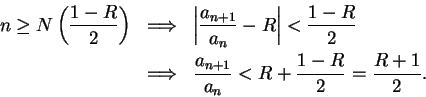
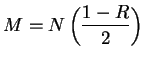 and
and
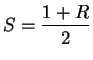 , so
, so
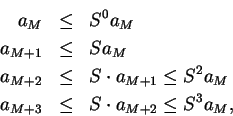
 . Then for all
. Then for all
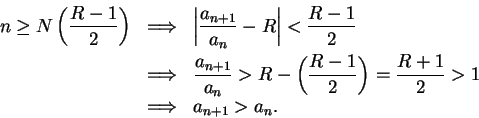
 for all
for all 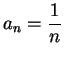 for
for
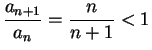 for all
for all 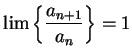 , and
the ratio test does not apply.)
, and
the ratio test does not apply.)
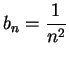 for all
for all
![]() , then
, then
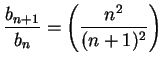 for all
for all ![]() and hence
and hence
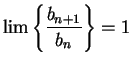 , and
, and ![]() is summable.
These examples show that when
is summable.
These examples show that when
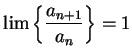 the
ratio test gives no useful information.
the
ratio test gives no useful information.
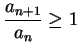 for all large
for all large 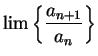 does not exist), since this
condition shows that
does not exist), since this
condition shows that 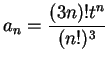 . We apply
the ratio test to the series
. We apply
the ratio test to the series ![\begin{displaymath}{{a_{n+1}}\over {a_n}}={{\left(3(n+1)\right)!t^{n+1}(n!)^3}\over
{[(n+1)!]^3(3n)!t^n}}.\end{displaymath}](img1497.gif)
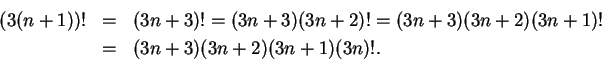
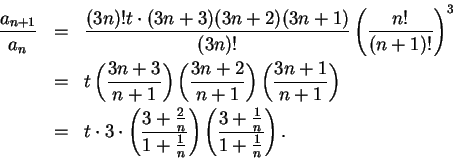
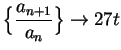 . The ratio test says that if
. The ratio test says that if 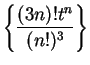 is summable, and
if
is summable, and
if
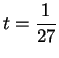 ? For
? For
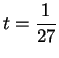 , our formula above gives us
, our formula above gives us
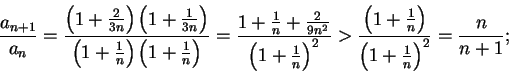
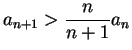 for
for 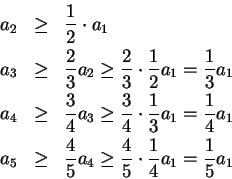
 is not summable, it follows
that
is not summable, it follows
that 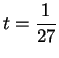 .
.
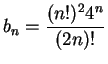 for all
for all
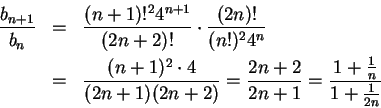
 and the ratio test does not
apply. But since
and the ratio test does not
apply. But since
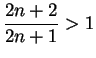 for all
for all 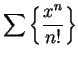
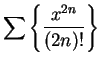
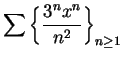
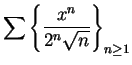
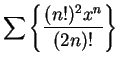 [For this series,
there is one
[For this series,
there is one