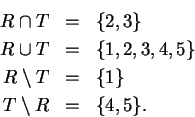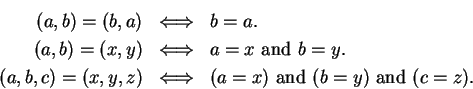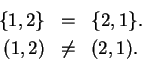Next: 1.5 Functions
Up: 1. Notation, Undefined Concepts
Previous: 1.3 Equality
Index
1.44
Definition (Proposition Form.)
Let
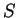
be a set. A
proposition form 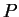
on
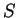
is a rule that assigns to
each element
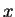
of
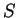
a unique proposition, denoted by
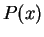
.
1.45
Examples.
Let
Then
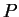
is a proposition form on
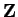
.
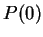
is false, and
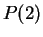
is true. Note
that
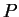
is neither true nor false. A proposition form is not a proposition.
Let
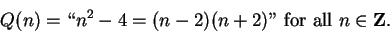 |
(1.46) |
Then
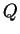
is a propostion form, and
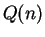
is true for all
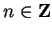
. Note that
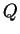
is not a proposition, but if
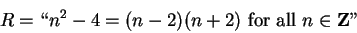 |
(1.47) |
then
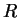
is a proposition and
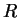
is true. Make sure that you see the difference
between the right sides of (
1.46) and (
1.47). The placement of the
quotation marks is crucial. When I define a proposition I will often
enclose it in quotation marks, to prevent ambiguity. Without the
quotation marks, I would not be able to distinguish between the right sides of
(
1.46) and (
1.47). If I see a statement like
without quotation marks, I immediately think this is a statement of the form
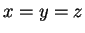
and conclude that
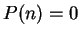
.
1.48
Notation.
Let
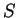
be a set, and let
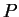
be a proposition form on
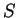
. Then
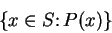 |
(1.49) |
denotes the set of all objects
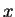
in
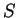
such that
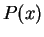
is true. (Read
(
1.49) as ``the set of all
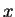
in
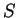
such that
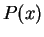
".)
Variations on this notation are common. For example,
represents the set of all numbers of the form 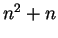 where
where
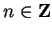 .
.
1.51
Definition (Union, intersection, difference.)
Let
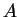
be a set, let
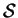
be the set of all subsets of
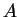
, and let
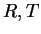
be
elements of
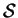
. We define the
intersection 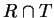
of
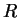
and
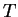
by
we define the
union 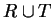
of
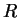
and
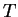
by
and we define the difference
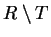
by
1.52
Examples.
If
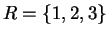
and
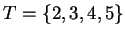
, then
1.53
Definition (Ordered pairs and triples.)
Let
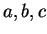
be objects (not necessarily all different). The ordered pair
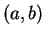
is
a set-like combination of
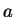
and
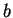
into a single object, in which
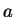
is
designated as the
first element and
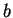
is designated as the
second
element. The ordered triple
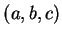
is a similar construction
having
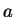
for its
first element,
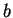
for its second element and
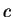
for its third element. Two ordered
pairs (triples) are equal if and only if they have the same first elements, the same
second elements, (and the same third elements). Thus
1.54
Warning.
Ordered pairs should not be confused with sets.
1.55
Definition (Cartesian product, 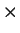 .)
.)
If
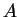
and
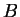
are sets, we define the set
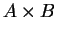
by
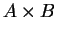
is called the
Cartesian Product of
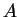
and
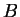
.
1.56
Example.
If
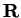
is the set of real numbers, then
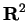
is the set of all ordered
pairs of real numbers. You are familiar with the fact that ordered pairs of real
numbers can be represented as points in the plane, so you can think of
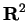
or
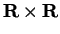
as being the points in the plane.




Next: 1.5 Functions
Up: 1. Notation, Undefined Concepts
Previous: 1.3 Equality
Index