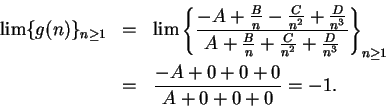Next: 10. The Derivative
Up: 9. Properties of Continuous
Previous: 9.1 Extreme Values
Index
9.11
Theorem (Intermediate Value Theorem.)
Let
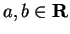 with
with 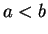 , and let
, and let
![$f\colon [a,b]\to\mbox{{\bf R}}$](img934.gif) be a
continuous function. Suppose
be a
continuous function. Suppose 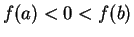 . Then there is some point
. Then there is some point 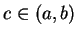 with
with 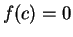 .
.
Proof: We will construct a binary search sequence ![$[a_n,b_n]$](img937.gif) with
with
![$[a_0,b_0]=[a,b]$](img936.gif) such that
such that
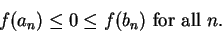 |
(9.12) |
Let
This is a binary search sequence satisfying condition (9.12).
Let 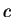 be the number such that
be the number such that
![$\{[a_n,b_n]\} \to c$](img493.gif) .
Then
.
Then 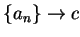 and
and 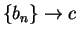 (cf theorem 7.87),
so by
continuity of
(cf theorem 7.87),
so by
continuity of  ,
,
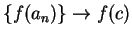 and
and
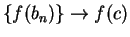 . Since
. Since 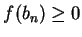 for all
for all 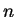 , it follows by the inequality theorem that
, it follows by the inequality theorem that
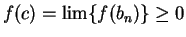 , and since
, and since 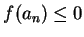 , we have
, we have
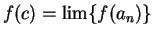
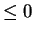 . Hence,
. Hence,
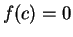 .
.

9.13
Exercise (Intermediate value theorem.)
A
Let
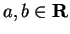
with
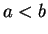
and let
![$f:[a,b]\to\mbox{{\bf R}}$](img983.gif)
be a continuous
function with
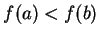
. Let
be a number in the interval
. Show that there is some
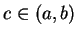
with
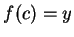
. (Use
theorem
9.11. Do not reprove it.)
9.14
Notation ( is between
is between  and
and 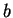 .)
.)
Let
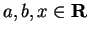
. I say
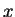
is
between 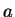
and
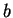
if either
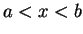
or
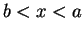
.
9.15
Corollary (Intermediate value theorem.)
Let
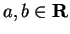 with
with 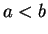 . Let
. Let
![$f\colon [a,b]\to\mbox{{\bf R}}$](img934.gif) be a continuous function with
be a continuous function with
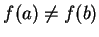 . If
. If 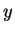 is any number between
is any number between 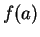 and
and 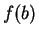 , then there is some
, then there is some
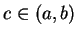 such that
such that 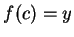 . In particular, if
. In particular, if 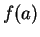 and
and 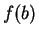 have opposite
signs, there is a number
have opposite
signs, there is a number 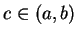 with
with 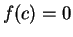 .
.
Proof: By exercise 9.13A, the result holds when 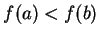 . If
. If
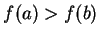 , let
, let 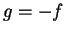 . Then
. Then 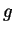 is continuous on
is continuous on ![$[a,b]$](img935.gif) and
and 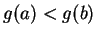 , so by
exercise 9.13A there is a
, so by
exercise 9.13A there is a 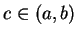 with
with 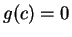 , so
, so 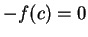 so
so
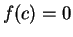 .
.

9.16
Example.
Let
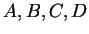
be real numbers with
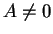
, and let
We will show that there is a number
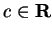
such that
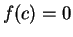
. Suppose, in order
to get a contradiction, that no such number
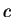
exists, and let
(I use the fact that
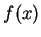
has no zeros here.) Then
It follows that
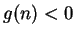
for some
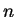
, so
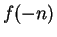
and
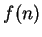
have opposite signs
for some
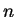
, and
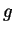
is continuous on
![$[-n,n]$](img1004.gif)
, so by the intermediate value
theorem,
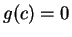
for some
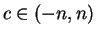
, contradicting the assumption that
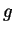
is never
zero.
9.18
Exercise.
Let
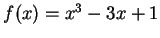
. Prove that the equation
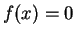
has at least three
solutions in
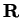
.
s
9.19
Exercise.
A
Let
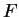
be a continuous function
from
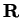
to
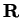
such that
- a)
- For all
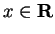 ,
,
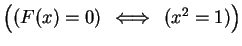 .
.
- b)
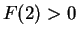 .
.
Prove that
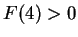
.
9.20
Note.
The intermediate value theorem was proved independently by
Bernhard Bolzano in
1817 [
42], and Augustin Cauchy in 1821[
23, pp 167-168]. The
proof we have given is almost identical with Cauchy's proof.
The extreme value theorem was proved by Karl
Weierstrass circa 1861.




Next: 10. The Derivative
Up: 9. Properties of Continuous
Previous: 9.1 Extreme Values
Index
![]() with
with
![]() such that
such that
![\begin{eqnarray*}[a_0,b_0]&=&[a,b] \cr
[a_{n+1},b_{n+1}]&=&\cases{ \left[a_n,{{a...
...er 2},b_n\right] &if
$f\left( {{a_n+b_n}\over 2}\right) <0$.\cr}
\end{eqnarray*}](img975.gif)
![]() be the number such that
be the number such that
![]() .
Then
.
Then ![]() and
and ![]() (cf theorem 7.87),
so by
continuity of
(cf theorem 7.87),
so by
continuity of ![]() ,
,
![]() and
and
![]() . Since
. Since ![]() for all
for all ![]() , it follows by the inequality theorem that
, it follows by the inequality theorem that
![]() , and since
, and since ![]() , we have
, we have
![]()
![]() . Hence,
. Hence,
![]() .
.
![]()
![]() . If
. If
![]() , let
, let ![]() . Then
. Then ![]() is continuous on
is continuous on ![]() and
and ![]() , so by
exercise 9.13A there is a
, so by
exercise 9.13A there is a ![]() with
with ![]() , so
, so ![]() so
so
![]() .
.
![]()