12.22
Example.
Suppose we had a complex function
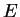
such that
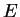
is everywhere differentable and
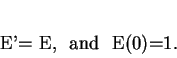 |
(12.23) |
Let
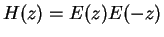
for all
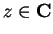
. By the chain and product rules,
on
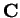
, so
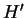
is constant. Since
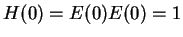
, we conclude
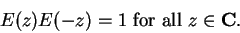 |
(12.24) |
In particular
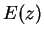
is never
, and
Now let
 and define a function
and define a function
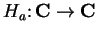 by
by
We have
for all
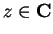
, so
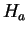
is constant, and
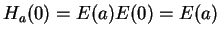
. Thus
and by (
12.24),
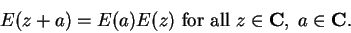 |
(12.25) |
Next suppose you know some function
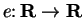
such that
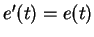
for
all
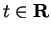
and
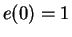
. (You do know such a function from your previous
calculus course.) Let
Then by the product and chain rules,
so
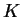
is constant on
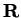
, and since
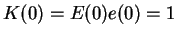
, we have
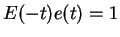
. By
(
12.24),
Now I will try to construct a function
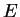
satisfying the differential equation
(
12.23)
by hoping that
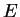
is given by a power series. Suppose
Since
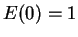
, we must have
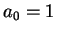
, and
By the differentiation theorem,
and
By the differentiation theorem again,
so
Hence
Repeating the process, we get
so
I see a pattern here:
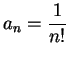
.
![]() and define a function
and define a function
![]() by
by
![\begin{eqnarray*}
H_a'(z)&=&E'(z+a)E(-z)+E(z+a)[-E'(-z)]\\
&=& E(z+a)E(-z) - E(z+a)E(-z) =0
\end{eqnarray*}](img1796.gif)
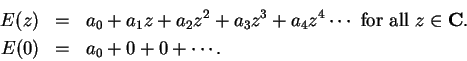
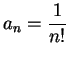 .
.
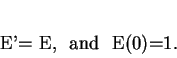
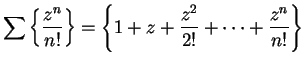 . We will show in exercise
. We will show in exercise 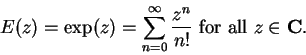
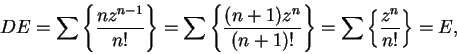
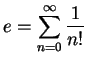 .
.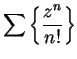 has infinite radius of
convergence.
has infinite radius of
convergence.
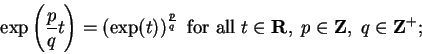
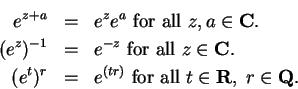
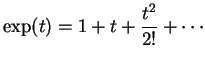 , we see that
, we see that 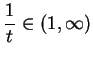 , so
, so
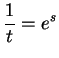 for some
for some