



Next: 1. Some Notation for
Up: 0. Introduction
Previous: Prerequisites
Index
The exercises are an important
part of the course.
Do not expect to be able to do all of them the
first time you try them, but you should understand them after
they have been discussed in class. Some important theorems will be proved in the
exercises. There are hints for some of the questions
in appendix A, but you should not look for a hint
unless you have made some effort to answer a question.
Sections whose titles are marked by an asterisk (e.g. section 2.6)
are not used later in the notes, and may be omitted. Hovever they contain
really neat material, so you will not want to omit them.
In addition to the exercises, there are some questions and
statements with the label ``entertainment''. These are
for people who find them entertaining.
They require more time and thought than the exercises.
Some of them
are more metaphysical than mathematical, and some of them require
the use of a computer or a programmable calculator.
If you do not find the entertainments entertaining, you may ignore them.
Here is one to start you off.
0.1
Entertainment (Calculation of  .)
.)
.
The area of a circle of radius 1 is denoted
by

. Calculate

as accurately as you can.
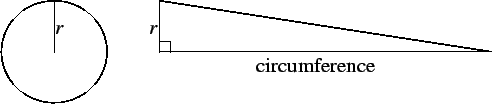
Archimedes showed that  is half of the circumference of a circle
of radius 1. More precisely, he showed that the area of a circle
is equal to the area of a triangle whose base is equal to the circumference
of the circle, and whose altitude is equal to the radius of the circle.
If we take a circle of radius 1, we get the result stated.
You should
assume Archimedes' theorem, and then entertainment 0.1
is equivalent to the
problem of calculating the circumference of a circle as accurately as you
can. An answer to this problem will be a pair of
rational numbers
is half of the circumference of a circle
of radius 1. More precisely, he showed that the area of a circle
is equal to the area of a triangle whose base is equal to the circumference
of the circle, and whose altitude is equal to the radius of the circle.
If we take a circle of radius 1, we get the result stated.
You should
assume Archimedes' theorem, and then entertainment 0.1
is equivalent to the
problem of calculating the circumference of a circle as accurately as you
can. An answer to this problem will be a pair of
rational numbers  and
and 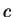 ,
together with an argument that
,
together with an argument that 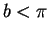 and
and 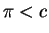 .
It is desired to make the
difference
.
It is desired to make the
difference 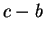 as small as possible.
as small as possible.
This problem is very old. The
Rhind Papyrus[16, page 92] (c. 1800 B.C.?)
contains the following rule for finding the area of a circle:
RULE I:
Divide the diameter of the circle into nine equal parts, and
form a square whose side is equal to eight of the parts. Then the
area of the square is equal to the area of the circle.
The early
Babylonians (1800-1600BC) [38, pages 47 and 51]
gave the following rule:
RULE II: The area of a circle is 5/60th of the square of the
circumference of the circle.
Archimedes (287-212 B.C.) proved
that the circumference of a circle is
three times the diameter plus a part smaller than one seventh of the diameter,
but
greater than 10/71 of the diameter[3, page 134].
In fact, by using only elementary geometry, he gave a method
by which  can be calculated to any degree of accuracy by someone
who can calculate square roots to any degree of accuracy. We do not
know how Archimedes calculated square roots, but people
have tried to figure out what method he used by the form of his
approximations. For example he says with no justification that
can be calculated to any degree of accuracy by someone
who can calculate square roots to any degree of accuracy. We do not
know how Archimedes calculated square roots, but people
have tried to figure out what method he used by the form of his
approximations. For example he says with no justification that
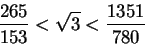
and
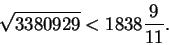
By using your calculator you can easily verify that these results are correct.
Presumably when you calculate  you will use a calculator or
computer to estimate any square roots you need. This immediately
suggests a new problem.
you will use a calculator or
computer to estimate any square roots you need. This immediately
suggests a new problem.
0.2
Entertainment (Square root problem.)
Write, or at least describe,
a computer program that will calculate square roots to a good deal
of accuracy. This program should use only the standard arithmetic
operations and the constructions available in all computer languages,
and should not use any special functions like square roots or logarithms.
An answer to this question must include some sort of explanation of
why the method works.
Zu Chongzhi (429-500 A.D.) stated
that  is between 3.1415926
and 3.1415927, and gave 355/113 as a good
approximation to
is between 3.1415926
and 3.1415927, and gave 355/113 as a good
approximation to  .[47, page 82]
.[47, page 82]
Here is a first approximation to  .
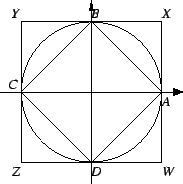
Consider a circle of radius 1 with center at
.
Consider a circle of radius 1 with center at  ,
and inscribe inside of it a square
,
and inscribe inside of it a square  of side
of side 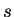 with vertices at
with vertices at
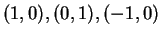 and
and 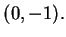 Then by the
Pythagorean theorem,
Then by the
Pythagorean theorem,
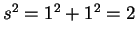 . But
. But 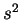 is the area of the
square
is the area of the
square 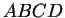 , and since
, and since 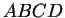 is contained inside of the circle we have
is contained inside of the circle we have
Consider also the circumscribed square 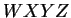 with horizontal and vertical
sides. This square has side 2,
and hence has area 4. Thus, since the circle is contained in
with horizontal and vertical
sides. This square has side 2,
and hence has area 4. Thus, since the circle is contained in  ,
,
It now follows that 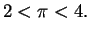
A number of extraordinary formulas for  are given in a recent paper
on How to Compute One Billion Digits of Pi[12].
One amazing formula given in this paper is the following result
are given in a recent paper
on How to Compute One Billion Digits of Pi[12].
One amazing formula given in this paper is the following result
which is due to S. Ramanujan(1887-1920)[12, p 201,p 215].
The reciprocal of the zeroth term of this
sum i.e.
gives a good approximation to  (see exercise 0.4).
(see exercise 0.4).
0.3
Exercise.
A
The formulas described in RULES I and II above
each determine an approximate value for

.
Determine the two approximate values. Explain your reasoning.
0.4
Exercise.
Use a calculator to find the value of
and compare this with the correct value of

, which is
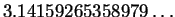
.




Next: 1. Some Notation for
Up: 0. Introduction
Previous: Prerequisites
Index
Ray Mayer
2007-09-07
![]() can be calculated to any degree of accuracy by someone
who can calculate square roots to any degree of accuracy. We do not
know how Archimedes calculated square roots, but people
have tried to figure out what method he used by the form of his
approximations. For example he says with no justification that
can be calculated to any degree of accuracy by someone
who can calculate square roots to any degree of accuracy. We do not
know how Archimedes calculated square roots, but people
have tried to figure out what method he used by the form of his
approximations. For example he says with no justification that
![]() is between 3.1415926
and 3.1415927, and gave 355/113 as a good
approximation to
is between 3.1415926
and 3.1415927, and gave 355/113 as a good
approximation to ![]() .[47, page 82]
.[47, page 82]
![]() .
Consider a circle of radius 1 with center at
.
Consider a circle of radius 1 with center at ![]() ,
and inscribe inside of it a square
,
and inscribe inside of it a square ![]() of side
of side ![]() with vertices at
with vertices at
![]() and
and ![]() Then by the
Pythagorean theorem,
Then by the
Pythagorean theorem,
![]() . But
. But ![]() is the area of the
square
is the area of the
square ![]() , and since
, and since ![]() is contained inside of the circle we have
is contained inside of the circle we have
![]()
![]() are given in a recent paper
on How to Compute One Billion Digits of Pi[12].
One amazing formula given in this paper is the following result
are given in a recent paper
on How to Compute One Billion Digits of Pi[12].
One amazing formula given in this paper is the following result
![\begin{displaymath}{1 \over \pi} = {\sqrt{8} \over 9801} \sum_{n=0}^\infty\frac{(4n)!}{(n!)^4}
\frac{ [1103 + 26390n]}{396^{4n}},\end{displaymath}](img76.gif)