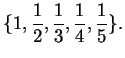 |
A set is any collection of objects. Usually
the objects we consider are things like numbers, points in the plane,
geometrical figures, or functions. Sets are often described
by listing the objects they contain inside curly braces, for
example
There are a few sets that occur very often in mathematics, and that have
special names:

A rational number is a number that can be
expressed as a quotient of two integers. Thus a real number ![]() is rational
if and only if there exist integers
is rational
if and only if there exist integers ![]() and
and ![]() with
with ![]() such that
such that
![]() .
.
The terms ``point in the plane'' and ``ordered pair of real numbers'' are taken to be synonymous. I assume that you are familiar with the usual representation of points in the plane by pairs of numbers, and the usual way of representing geometrical objects by equations and inequalities.
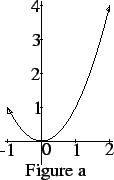
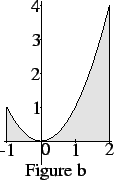
Thus the set of points ![]() such that
such that
![]() is represented in figure a, and the set of points
is represented in figure a, and the set of points ![]() such that
such that
![]() and
and
![]() is represented
in figure b. The arrowheads in figure a indicate that only part of
the figure has been drawn.
is represented
in figure b. The arrowheads in figure a indicate that only part of
the figure has been drawn.
The objects in a set ![]() are called elements of
are called elements of ![]() or points
in
or points
in ![]() . If
. If ![]() is an object and
is an object and ![]() is a set then
is a set then
and

To see that
![]() observe that
observe that ![]() has exactly four
elements, and none of these elements is
has exactly four
elements, and none of these elements is ![]()
Let ![]() and
and ![]() be sets. We say that
be sets. We say that ![]() is a subset
of
is a subset
of ![]() and write
and write ![]() if and only if every element in
if and only if every element in ![]() is also in
is also in ![]() Two sets are considered to be equal if and
only if they have exactly the same elements. Thus
Two sets are considered to be equal if and
only if they have exactly the same elements. Thus
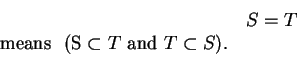
In the examples above, ![]() and
and ![]() For every set
For every set ![]() we have
we have

The idea of set was introduced into mathematics by Georg Cantor near
the end of the nineteenth century. Since then it has become one of the
most important ideas in mathematics. In these notes we use
very little from the theory of sets, but the language of
sets will be very evident.
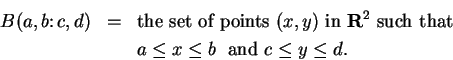
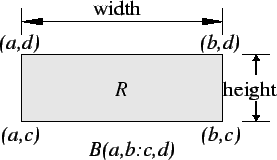
Remark: Notice that in the definition of box, the inequalities
are ``![]() '' and not ``
'' and not ``![]() ''. The choice of which sort of inequality
to use is somewhat arbitrary, but some of the assertions we will
be making about boxes would turn out to be false if the boxes did
not contain their boundaries.
''. The choice of which sort of inequality
to use is somewhat arbitrary, but some of the assertions we will
be making about boxes would turn out to be false if the boxes did
not contain their boundaries.
In Euclid's geometry no distinction is made between sets that contain their boundaries and sets that do not. In fact the early Greek geometers did not think in terms of sets at all. Aristotle maintained that
A line cannot be made up of points, seeing that a line is a continuous thing, and a point is indivisible[25, page 123].The notion that geometric figures are sets of points is a very modern one. Also the idea that area is a number has no counterpart in Euclid's geometry, and in fact Euclid does not talk about area at all. He makes statements like
Triangles which are on equal bases and in the same parallels are equal to one another[17, vol I page 333].We interpret ``are equal to one another'' to mean ``have equal areas'', but Euclid does not define ``equal'' or mention ``area''.
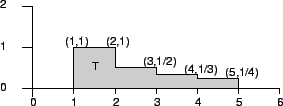
The intersection of the sets
![]() is defined to be
the
set of points
is defined to be
the
set of points ![]() that are in every one of the sets
that are in every one of the sets ![]() . This intersection
is denoted by
. This intersection
is denoted by
The index ![]() in equations 1.3 and 1.4 is called a
dummy index and it can be replaced by any symbol that
does not
have a meaning assigned to it. Thus,
in equations 1.3 and 1.4 is called a
dummy index and it can be replaced by any symbol that
does not
have a meaning assigned to it. Thus,
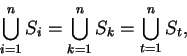
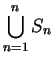 or
or
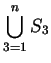 will
be considered to be ungrammatical.
will
be considered to be ungrammatical.
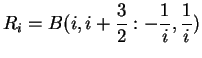 .
Then
.
Then
 .
Also
.
Also
 .
.
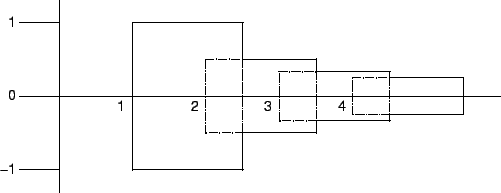
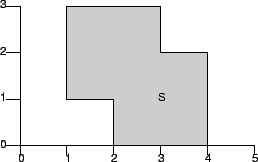
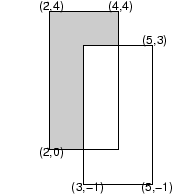
In the figure below,
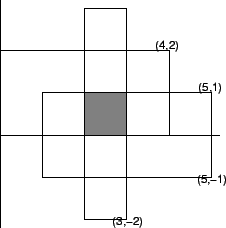
In the figure, the shaded region represents
![]() .
.
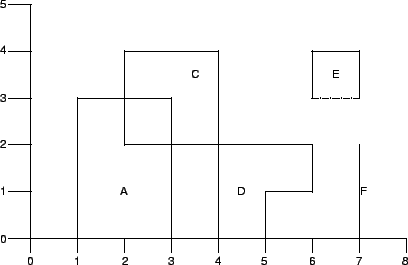
I will often use set relations such as

a) Express each of ![]() ,
, ![]() ,
, ![]() in the form
in the form ![]() .
.
b) Express ![]() ,
, ![]() , and
, and ![]() as intersections or unions
or set differences of boxes. The dotted edge
of
as intersections or unions
or set differences of boxes. The dotted edge
of ![]() indicates that the edge is missing from the set.
indicates that the edge is missing from the set.
c) Find a box that contains ![]() .
.
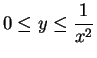 .
Let
.
Let