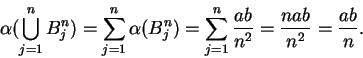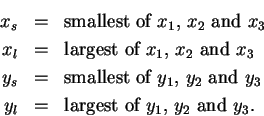Next: 5.4 Logarithms.
Up: 5. Area
Previous: 5.2 Further Assumptions About
Index
5.27
Definition (Partition.)
Let
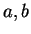
be
real
numbers with
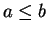
.
A
partition 
of the interval
![$[a,b]$](img1071.gif)
is a finite sequence of points
with
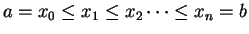
. The intervals
![$[x_0,x_1],[x_1,x_2],\cdots$](img1114.gif)
,
![$[x_{n-1},x_n]$](img1115.gif)
are called the
subintervals of
the
partition 
, and
![$[x_{j-1},x_j]$](img1116.gif)
is the
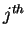 subinterval of
subinterval of 
for
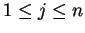
. The largest of the numbers
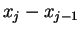
is called the
mesh
of the partition 
, and is denoted by
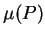
. The partition
is called the
regular partition of ![$[a,b]$](img1071.gif) into
into  equal
subintervals.
equal
subintervals.
5.28
Example.
Let
Then

is a partition of
![$[0,1]$](img908.gif)
into
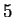
subintervals and
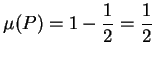
.
The regular partition of ![$[1,2]$](img1125.gif) into
into 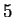 subintervals is
subintervals is
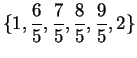 .
.
If 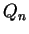 is the regular partition of
is the regular partition of ![$[a,b]$](img1071.gif) into
into  equal subintervals, then
equal subintervals, then
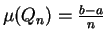 .
.
5.29
Exercise.
Find a partition

of
![$[0,1]$](img908.gif)
into five
subintervals, such that
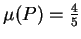
, or explain why no such partition exists.
5.30
Exercise.
Find a partition
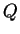
of
![$[0,1]$](img908.gif)
into five
subintervals, such that
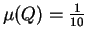
, or explain why no such partition exists.
5.31
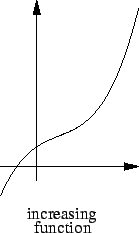
Definition (Monotonic function.)
Let

be an interval in
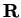
, and let
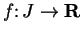
be a function. We say that

is
increasing on 
if
![\begin{displaymath}\mbox{ for all }x,y \mbox{ in } J \Big[(x\leq y)\mbox{$\hspac...
...rightarrow\hspace{1ex}$}(f(x) \leq f(y))\Big]\mbox{{\nonumber}}\end{displaymath}](img1133.gif) |
(5.32) |
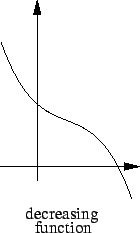
and we say that

is
decreasing on 
if
We say that

is
strictly increasing on 
if
and we say that

is
strictly decreasing on 
if
We say that

is
monotonic on J if

is either increasing on

or decreasing on

, and we say that

is
strictly monotonic on

if

is either strictly increasing or strictly decreasing on

.
A constant function on  is both increasing and
decreasing on
is both increasing and
decreasing on  .
.
5.33
Notation ( )
)
Let

be a function from the interval
![$[a,b]$](img1071.gif)
to the non-negative
numbers. We will write
i.e.,
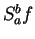
is the set of points under the graph of

over the interval
![$[a,b]$](img1071.gif)
.
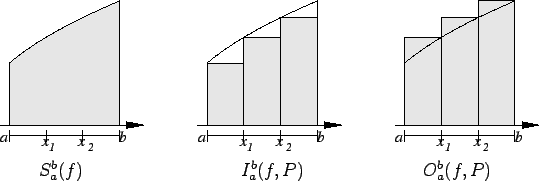
Let  be an increasing function
from the interval
be an increasing function
from the interval ![$[a,b]$](img1071.gif) to the non-negative
numbers.
Let
to the non-negative
numbers.
Let
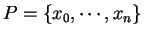 be a partition of
be a partition of ![$[a,b]$](img1071.gif) and let
and let
Then
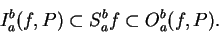 |
(5.34) |
To see this, observe that since  is increasing
is increasing
so
and also
By equation (5.34) and monotonicity of area, we have
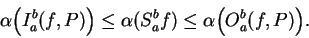 |
(5.35) |
Now
Now let 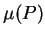 be the mesh of
be the mesh of  (cf. definition 5.27) so that
(cf. definition 5.27) so that
Since
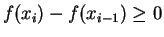 for all
for all 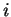 , we have
, we have
for all 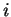 , and hence
, and hence
Now
so by equations (5.37) and (5.36), we have
Now suppose that  is any real number that satisfies
is any real number that satisfies
We will show that
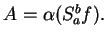 We have
We have
It follows from (5.35) that
Thus
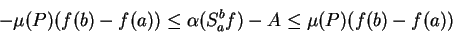 |
(5.38) |
for every partition  of
of ![$[a,b]$](img1071.gif) . Since we can find partitions
. Since we can find partitions  with
with  smaller than any preassigned number, it follows that
smaller than any preassigned number, it follows that
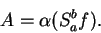 |
(5.39) |
(After we have discussed the notion of limit, we will come back
and reconsider how (5.39) follows from (5.38).
For the present, I will just say that the implication is intuitively
clear.)
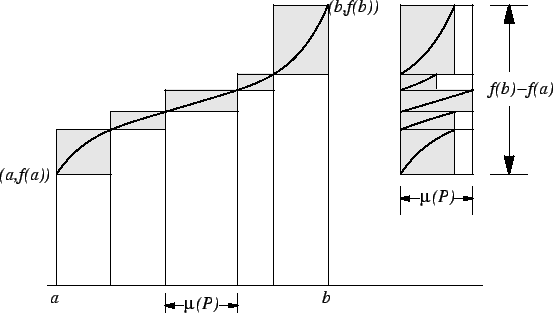
We have now proved the following theorem:
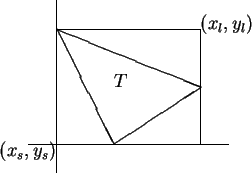
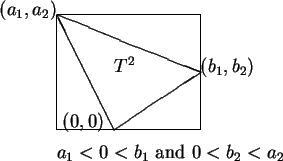
5.40
Theorem.
Let

be an increasing function from the interval
![$[a,b]$](img1071.gif)
to
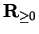
,
and let
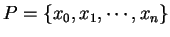
be a
partition
of
![$[a,b]$](img1071.gif)
. Let
Then
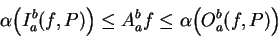 |
(5.43) |
and
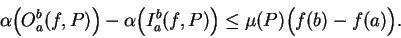 |
(5.44) |
Also
If

is any real number such that
then
The following picture illustrates the previous theorem.
5.47
Exercise.
A version of theorem
5.40 for decreasing functions is also
valid.
To get this version you should replace the word ``increasing" by ``decreasing"
and change lines (
5.41), (
5.42), (
5.44),
(
5.45) and
(
5.46).
Write down the proper versions of the altered lines. As usual, use
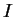
to
denote
areas inside
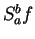
and
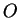
to denote sets containing
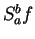
. Draw a
picture
corresponding to the above figure for a decreasing function.
5.49
Remark.
We know from Euclidean geometry that
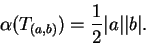 |
(5.50) |
I would like to show that this relation follows from our
assumptions about area. If
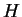
,
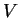
and
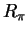
are
the reflections and rotation defined in definition
4.9, then we can
show without difficulty that for
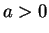
and
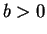
so by invariance of area under symmetry,
when

and

are positive.
It follows that if we prove formula (
5.50) when

and

are positive, then the formula holds in all cases.
For example if

and

are positive, and we know that
(
5.50) holds when

and

are positive, we get
and thus our formula holds when

is negative and

is positive.
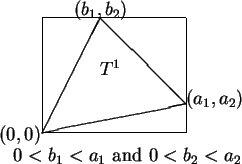
5.51
Theorem.
Let

and

be non-zero real numbers, and let
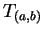
be the set defined in definition
5.48.
Then
Proof: By the previous remark, if is sufficient to prove the theorem
for the case when  and
and  are positive. So suppose that
are positive. So suppose that  and
and  are positive.
are positive.
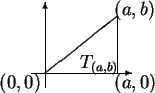
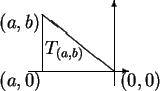
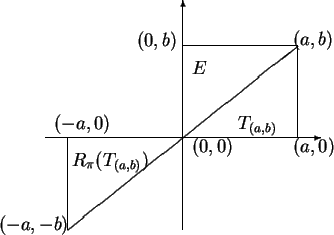
Let
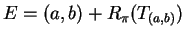 . It appears from the figure,
and is straightforward to show, that
. It appears from the figure,
and is straightforward to show, that
By translation invariance of area,
We have
and
By the
addition rule for area (assumption 5.14) we have
i.e.,
Thus our theorem will follow if we can show that the
segment
![$[{\bf0}\mathbf{{\bf c}}]$](img1188.gif) is a zero-area set.
We will prove this as the next theorem.
is a zero-area set.
We will prove this as the next theorem.
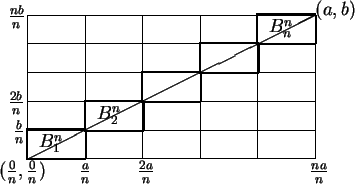
5.52
Theorem.
Let
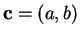
be a point in

.
Then
Proof: If 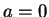 or
or 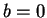 , then
, then
![${[{\bf0}\mathbf{{\bf c}}]}$](img1222.gif) is a box with width equal to zero, or height equal to zero, so
the theorem holds in this case. Hence we only need to consider the case
where
is a box with width equal to zero, or height equal to zero, so
the theorem holds in this case. Hence we only need to consider the case
where  and
and  are non-zero. Since any segment
are non-zero. Since any segment
![$[{\bf0}\mathbf{{\bf c}}]$](img1188.gif) can be rotated or reflected to a segment
can be rotated or reflected to a segment
![$[{\bf0}\mbox{{\bf q}}]$](img1223.gif) where
where
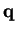 is in the first quadrant, we may further assume
that
is in the first quadrant, we may further assume
that  and
and  are both positive. Let
are both positive. Let  be a positive integer,
and for
be a positive integer,
and for
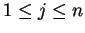 let
let
Then
![\begin{displaymath}
{[}{\bf0}\mathbf{{\bf c}}] \subset \bigcup_{j=1}^n B^n_j,
\end{displaymath}](img1227.gif) |
(5.53) |
since
For each 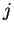 we have
we have
Also the sets 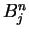 and
and 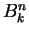 are almost disjoint whenever
are almost disjoint whenever
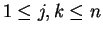 and
and 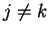 . (If
. (If 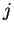 and
and 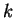 differ by more than 1,
then
differ by more than 1,
then 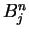 and
and 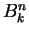 are disjoint, and if
are disjoint, and if 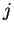 and
and 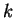 differ
by 1, then
differ
by 1, then
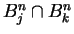 consists of a single point.)
By additivity for almost-disjoint sets (assumption 5.25), it
follows that
consists of a single point.)
By additivity for almost-disjoint sets (assumption 5.25), it
follows that
By (5.53) and monotonicity of area we have
![\begin{displaymath}
\alpha([0\mathbf{{\bf c}}]) \leq \alpha(\bigcup_{j=1}^n B^n_j) = {ab\over n}
\mbox{ for every positive integer } n.
\end{displaymath}](img1236.gif) |
(5.54) |
In order to conclude from this that
![$\alpha([{\bf0}\mathbf{{\bf c}}]) = 0$](img1237.gif) We now make use of the
Archimedean property
of the real numbers,
which says that for
any real number
We now make use of the
Archimedean property
of the real numbers,
which says that for
any real number  there is a positive integer
there is a positive integer  with
with 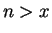 .
We know
.
We know
![$\alpha([{\bf0}\mathbf{{\bf c}}])\geq 0$](img1239.gif) , since all areas are non-negative.
Suppose (in order to get a contradiction) that
, since all areas are non-negative.
Suppose (in order to get a contradiction) that
![$\alpha([{\bf0}\mathbf{{\bf c}}])$](img1240.gif) is positive. Then by the Archimedean property, there is a
positive integer
is positive. Then by the Archimedean property, there is a
positive integer 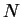 such that
such that
![$N > {ab\over \alpha([{\bf0}\mathbf{{\bf c}}])}$](img1241.gif) . This implies
that
. This implies
that
![$\alpha([{\bf0}\mathbf{{\bf c}}]) > {ab\over N}$](img1242.gif) ,
and this contradicts (5.54). Hence
,
and this contradicts (5.54). Hence
![$\alpha([{\bf0}\mathbf{{\bf c}}])$](img1240.gif) is not positive, and we conclude that
is not positive, and we conclude that
![$\alpha([{\bf0}\mathbf{{\bf c}}]) = 0$](img1237.gif) .
. 
Archimedes' statement of the Archimedean property differs from
our statement. He assumes that
Further, of unequal lines, unequal surfaces, and unequal solids,
the greater exceeds the less by such a magnitude
as, when added to itself, can be made to exceed any assigned
magnitude among those which are comparable with [it and with] one
another.[2, page 4]
5.55
Exercise.
Let
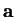
and
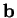
be points in

. Show that
segment
![$[\mbox{{\bf a}}\mbox{{\bf b}}]$](img864.gif)
is a zero are set. (Use theorem
5.52. Do not reprove theorem
5.52).
5.56
Entertainment (Area of a triangle)
Let
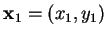
,
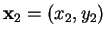
and
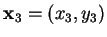
be three points in

, and let
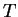
be the triangle
with vertices
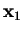
,
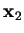
and
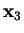
. Let
Then the box
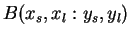
is an almost-disjoint
union of
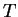
and three triangles which are translates
of triangles of the form
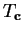
.
Since you know how to find the area of a box and
of a triangle
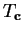
, you can find the area of
.
Using this remark show that for the triangles pictured
below,
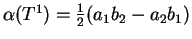
, and
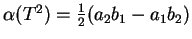
.
Then choose another triangle
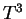
with vertices
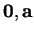
and
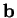
, where the coordinates of the points
are related in a way different from the ways shown for
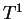
and
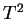
,
and calculate the area of
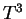
. You
should find that
in all cases. Notice that if some coordinate is zero, the formula agrees
with theorem
5.51.




Next: 5.4 Logarithms.
Up: 5. Area
Previous: 5.2 Further Assumptions About
Index
Ray Mayer
2007-09-07
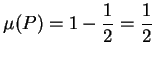 .
.
![]() into
into ![]() subintervals is
subintervals is
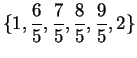 .
.
![]() is the regular partition of
is the regular partition of ![]() into
into ![]() equal subintervals, then
equal subintervals, then
![]() .
.
![]() is both increasing and
decreasing on
is both increasing and
decreasing on ![]() .
.
![]() be an increasing function
from the interval
be an increasing function
from the interval ![]() to the non-negative
numbers.
Let
to the non-negative
numbers.
Let
![]() be a partition of
be a partition of ![]() and let
and let
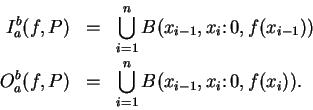
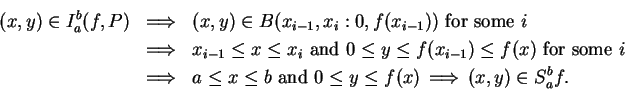
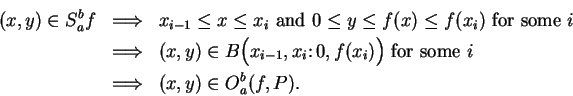
![]() and
and ![]() , then
, then
![]()
![]() and
and ![]() , then
, then
![]()
![]() and
and ![]() , then
, then
![]()
![]() and
and ![]() , then
, then
![]()
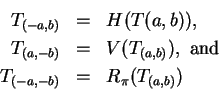
![]() and
and ![]() are positive. So suppose that
are positive. So suppose that ![]() and
and ![]() are positive.
are positive.
![\begin{eqnarray*}
ab &=& \alpha(B(0,a:0,b))\\
&=& \alpha( E \cup T_{(a,b)} ) ...
...)})\\
&=& 2\alpha(T_{(a,b)}) -\alpha([{\bf0}\mathbf{{\bf c}}]),
\end{eqnarray*}](img1217.gif)
![]() or
or ![]() , then
, then
![]() is a box with width equal to zero, or height equal to zero, so
the theorem holds in this case. Hence we only need to consider the case
where
is a box with width equal to zero, or height equal to zero, so
the theorem holds in this case. Hence we only need to consider the case
where ![]() and
and ![]() are non-zero. Since any segment
are non-zero. Since any segment
![]() can be rotated or reflected to a segment
can be rotated or reflected to a segment
![]() where
where
![]() is in the first quadrant, we may further assume
that
is in the first quadrant, we may further assume
that ![]() and
and ![]() are both positive. Let
are both positive. Let ![]() be a positive integer,
and for
be a positive integer,
and for
![]() let
let
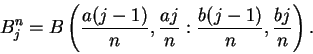
![\begin{eqnarray*}
\mbox{{\bf x}}\in [{\bf0}\mathbf{{\bf c}}] &\mbox{$\Longrighta...
...box{{\bf x}}\in B^n_j \mbox{ for some $j$ with } 1\leq j\leq n.
\end{eqnarray*}](img1228.gif)