



Next: 4.3 The Pythagorean Theorem
Up: 4. Analytic Geometry
Previous: 4.1 Addition of Points
Index
4.9
Definition (Reflections and Rotations.)
We now define a family of functions from

to

. If
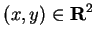
, we define
Each of the eight functions just defined carries every box to another box with
the
same area. You should be able to see from the picture that
We can see this analytically as follows:
I will usually omit the analytic justification in cases like this.
Each of the eight functions described in definition 4.9
carries
the
square
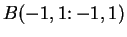 to itself.
to itself.
4.12
Definition (Symmetry of the square.)
The eight functions defined in equations (
4.10)-(
4.11)
are called
symmetries of the square.
4.13
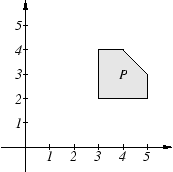
Exercise.
Let
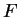
be the set shown in the figure. On one set of axes draw the sets
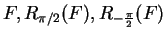
and
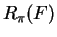
(label the four sets). On
another set of axes draw and label the sets
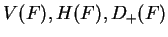
and
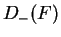
.
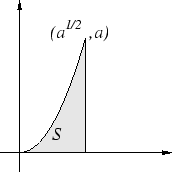
4.14
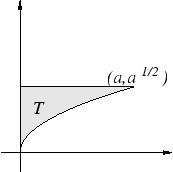
Example.
Let
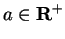
and let
From the picture it is clear that
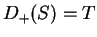
. An analytic proof of this result
is
as follows:
To show that
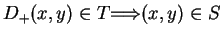
, I need to show that (
4.16)
implies
(
4.15). This follows because
In exercise
2.18
you assumed that

and
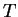
have the same area. In
general we will assume that if

is a set and
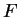
is a symmetry of
the square,
then

and
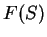
have the same area.
(Cf. Assumption
5.11.)
4.17
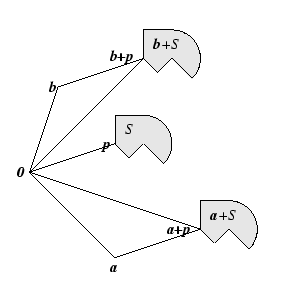
Definition (Translate of a set.)
Let

be a set in

and let
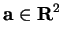
. We define the set
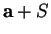
by
Sets of the form
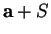
will be called
translates of 
.
4.18
Example.
The pictures below show some examples of translates. Intuitively each
translate of

has the same shape as

and each translate of

has the
same
area as

.
4.19
Example (Translates of line segments.)
Let
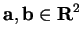
.
If
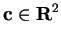
, then
In particular
![$-\mbox{{\bf a}}+[\mbox{{\bf a}},\mbox{{\bf b}}]=[\mbox{{\bf0}},\mbox{{\bf b}}-\mbox{{\bf a}}]$](img956.gif)
, so any segment can be
translated
to a segment with
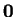
as an endpoint.
4.20
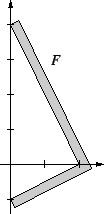
Exercise.
Let
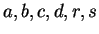
be real numbers with
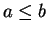
and
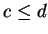
. Show
that
if the four question marks are replaced by suitable expressions. Include some
explanation for your answer.
4.21
Exercise.
Let

be the set shown in the figure below.
a) Sketch the sets 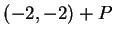 and
and 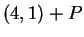 .
.
b) Sketch the sets
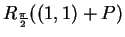 and
and
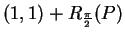 ,
where
,
where
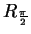 is defined as in definition 4.9
is defined as in definition 4.9




Next: 4.3 The Pythagorean Theorem
Up: 4. Analytic Geometry
Previous: 4.1 Addition of Points
Index
Ray Mayer
2007-09-07
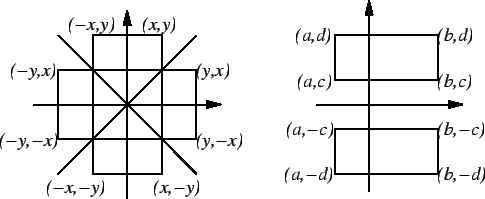
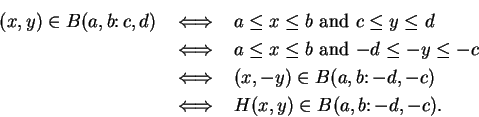
![]() to itself.
to itself.
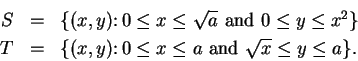
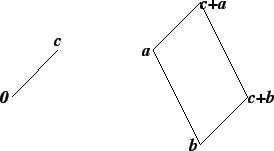
![\begin{eqnarray*}
\mathbf{{\bf c}}+[\mbox{{\bf a}}\mbox{{\bf b}}] &=& \mathbf{{\...
...thbf{{\bf c}}+\mbox{{\bf a}})(\mathbf{{\bf c}}+\mbox{{\bf b}})].
\end{eqnarray*}](img954.gif)
![]() and
and ![]() .
.
![]() and
and
![]() ,
where
,
where
![]() is defined as in definition 4.9
is defined as in definition 4.9