



Next: 5.2 Further Assumptions About
Up: 5. Area
Previous: 5. Area
Index
5.1 Basic Assumptions about Area
5.3
Definition (Bounded Sets.)
A subset

of

is
bounded if
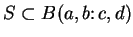
for some box
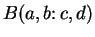
. A subset of

that is not bounded is said to be
unbounded.
It is clear that every subset of a bounded set is bounded. It is not
difficult to show that if 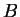 is a bounded set then
is a bounded set then
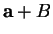 is bounded for every
is bounded for every
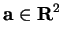 , and
, and
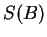 is bounded for every symmetry of the square,
is bounded for every symmetry of the square,  .
.
5.4
Example.
The set
is an unbounded subset of

. I cannot draw a picture of an
unbounded set, because the sheet of paper on which I make my
drawing will represent a box containing any picture I draw.
5.5
Definition (Bounded Function.)
Let

be a set. A function
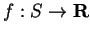
is called a
bounded function if there is a number
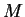
such that
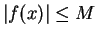
for all
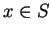
. It is clear that
if

is a bounded function on an interval
![$[a,b]$](img1071.gif)
, then graph
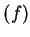
is
a bounded subset of

, since graph
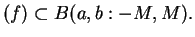
If

is bounded on

, then any number
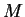
satisfying
is called a
bound for 
on

.
We are now ready to state our official assumptions about area. At this point
you
should officially forget everything you know about area. Unofficially,
however, you
remember everything you know so that you can evaluate whether the theorems we
prove are reasonable. Our aim is not simply to calculate areas,
but to see how our
calculations are justified by our assumptions.
We will assume that there is a function 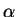 from the set of bounded
subsets of
from the set of bounded
subsets of
 to the real numbers that satisfies the conditions of positivity,
additivity,
normalization, translation invariance and symmetry invariance described below.
Any
function
to the real numbers that satisfies the conditions of positivity,
additivity,
normalization, translation invariance and symmetry invariance described below.
Any
function 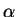 that satisfies these conditions will be called an area
function.
that satisfies these conditions will be called an area
function.
5.6
Assumption (Positivity of area.)
5.7
Definition (Disjoint sets.)
We say two sets
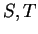
are
disjoint if and only
if
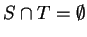
.
5.8
Assumption (Additivity of area.)
If
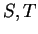
are disjoint bounded subsets of

,
then
5.9
Assumption (Normalization property of area.)
For every box
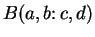
we have
i.e., the area of a box is the product of the length and the width of the box.
5.10
Assumption (Translation invariance of area.)
Let

be a bounded set in

,
and
let
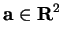
, then
5.11
Assumption (Invariance under symmetry.)
Let

be a bounded subset of

.
Then
if
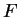
is any symmetry of the square
(See definition
4.12 for the definition of symmetry of the square.)
Remark: I would like to replace the assumptions 5.10
and 5.11 by the single stronger assumption:
If  and
and 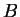 are bounded subsets of
are bounded subsets of
 , and
, and  is congruent to
is congruent to 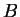 ,
then
,
then
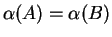 .
.
However the problem of defining what congruent means is rather
complicated, and I do not want to consider it at this point.
5.12
Entertainment (Congruence problem.)
Formulate a
definition of what it means for two subsets of

to be
congruent.
5.13
Example.
Let
I do not know how to make any reasonable drawing of

or
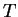
. Any picture
I draw of

would look just like a picture of
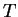
, even though the
two sets are disjoint.
By additivity and the normalization property for area
Since areas are non-negative, it follows that
The problem of calculating
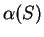
exactly cannot be answered on the
basis of the assumptions we have made.
Remarks: The assumptions we have just made are supposed to be
intuitively plausible. When we choose to make a particular set of assumptions,
we
hope that the assumptions are consistent, i.e., that no contradictions follow
from them. If we were to add a new assumption:
then we would have an inconsistent set of assumptions, because it follows from
the
assumptions we have already made that the area of a circle of radius 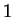 is
greater
than
is
greater
than 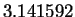 .
.
In 1923 Stefan Banach(1892-1945)
[5] showed that area functions exist, i.e., that the
assumptions we have made about area are consistent. Unfortunately
Banach showed that there is more than one area function, and
different area functions assign different values to the set  described in the previous example.
described in the previous example.
A remarkable result of
Felix Hausdorff(1868-1942)
[24, pp469-472] shows that the analogous assumptions for volume in three
dimensional space (if we include the assumption that any two congruent sets in
3 dimensional space
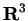 have the same volume) are inconsistent. If one
wants to
discuss volume in
have the same volume) are inconsistent. If one
wants to
discuss volume in
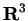 then one cannot consider volumes of arbitrary sets.
One
must considerably restrict the class of sets that have volumes. A discussion
of Hausdorff's result can be found in [20].
then one cannot consider volumes of arbitrary sets.
One
must considerably restrict the class of sets that have volumes. A discussion
of Hausdorff's result can be found in [20].




Next: 5.2 Further Assumptions About
Up: 5. Area
Previous: 5. Area
Index
Ray Mayer
2007-09-07
![]() from the set of bounded
subsets of
from the set of bounded
subsets of
![]() to the real numbers that satisfies the conditions of positivity,
additivity,
normalization, translation invariance and symmetry invariance described below.
Any
function
to the real numbers that satisfies the conditions of positivity,
additivity,
normalization, translation invariance and symmetry invariance described below.
Any
function ![]() that satisfies these conditions will be called an area
function.
that satisfies these conditions will be called an area
function.
and
are bounded subsets of
, and
is congruent to
, then
.
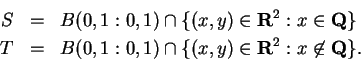
![]() described in the previous example.
described in the previous example.
![]() have the same volume) are inconsistent. If one
wants to
discuss volume in
have the same volume) are inconsistent. If one
wants to
discuss volume in
![]() then one cannot consider volumes of arbitrary sets.
One
must considerably restrict the class of sets that have volumes. A discussion
of Hausdorff's result can be found in [20].
then one cannot consider volumes of arbitrary sets.
One
must considerably restrict the class of sets that have volumes. A discussion
of Hausdorff's result can be found in [20].