



Next: 5.1 Basic Assumptions about
Up: Math 111 Calculus I
Previous: 4.3 The Pythagorean Theorem
Index
5. Area
In chapter 2 we calculated the area of the set
where 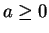 , and of the set
, and of the set
where 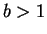 .
.
The technique that was used for making
these
calculations can be used to find the areas of many other subsets of
 .
The
general procedure we will use for finding the area of a set
.
The
general procedure we will use for finding the area of a set  will be to find
two
sequences of polygons
will be to find
two
sequences of polygons 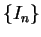 and
and 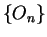 such that
such that
We will then have
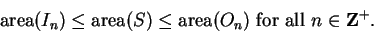 |
(5.1) |
We will construct the polygons 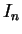 and
and 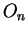 so that
so that
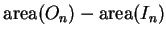 is
arbitrarily small when
is
arbitrarily small when  large enough, and we will see that then there is a
unique
number
large enough, and we will see that then there is a
unique
number  such that
such that
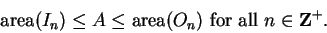 |
(5.2) |
We will take  to be the area of
to be the area of  .
.
Subsections




Next: 5.1 Basic Assumptions about
Up: Math 111 Calculus I
Previous: 4.3 The Pythagorean Theorem
Index
Ray Mayer
2007-09-07
![]() .
The
general procedure we will use for finding the area of a set
.
The
general procedure we will use for finding the area of a set ![]() will be to find
two
sequences of polygons
will be to find
two
sequences of polygons ![]() and
and ![]() such that
such that