The following calculation of ![]() is due to William Brouncker
(1620-1684)[22, page 54].
is due to William Brouncker
(1620-1684)[22, page 54].
Let
![]() denote the
regular partition of the interval
denote the
regular partition of the interval ![]() into
into ![]() equal subintervals.
Let
equal subintervals.
Let
![\begin{displaymath}K(2^n) = I_1^2(\Big[{1\over t}\Big], P_{2^n})
= \bigcup_{i=1}^{2^n} B(x_{i-1},x_i;0,{1\over x_i}). \end{displaymath}](img1372.gif)
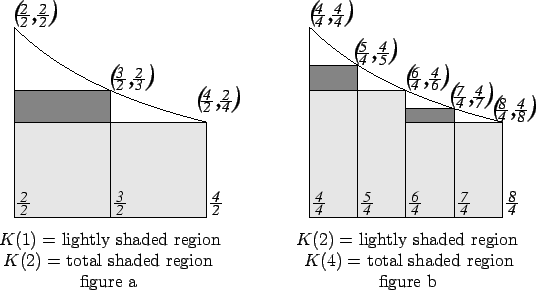
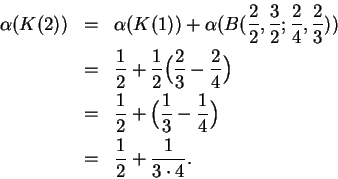
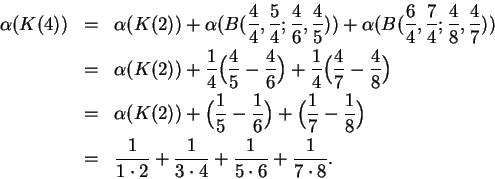
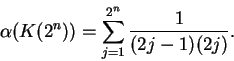
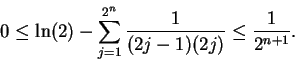
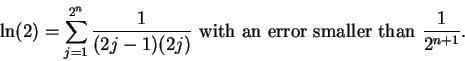
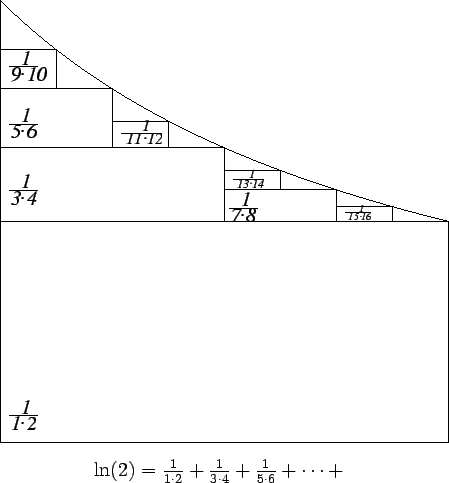
Equation (5.82) is sometimes called Mercator's expansion for
![]() , after Nicolaus Mercator,
who found the result sometime near 1667 by an entirely different
method.
, after Nicolaus Mercator,
who found the result sometime near 1667 by an entirely different
method.
Brouncker's calculation was published in 1668, but was done about ten years earlier [22, pages 56-56].
Brouncker's formula above is an elegant result, but it is
not very
useful for calculating: it takes too many terms in the sum to get much
accuracy.
Today, when a logarithm can be found by pressing a button on a calculator,
we tend to think of ``![]() " as being a known number, and of Brouncker's
formula
as giving a ``closed form" for the sum of the infinite series
" as being a known number, and of Brouncker's
formula
as giving a ``closed form" for the sum of the infinite series
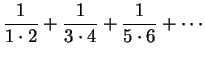 .
.