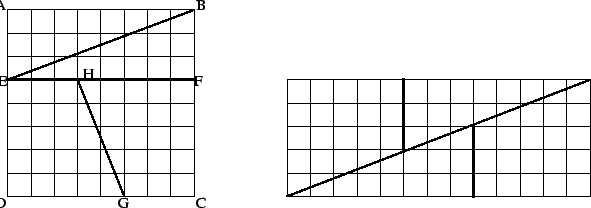
If ![]() is the set of points
is the set of points ![]() in
in
![]() such that
such that ![]() and
and
![]() , then we showed in (2.6) that
, then we showed in (2.6) that
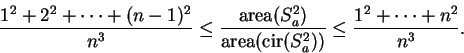
The right side of (2.13) is greater than
![]() and the
left side is less than
and the
left side is less than
![]() for all
for all
![]() , but by taking
, but by taking
![]() large enough, both sides can be made as close to
large enough, both sides can be made as close to
![]() as
we please. Hence we conclude that the ratio
as
we please. Hence we conclude that the ratio
 is equal to
is equal to
![]() . Thus, we have proved the following theorem:
. Thus, we have proved the following theorem:

Remark: The last paragraph of the proof of theorem 2.14 is a little bit vague. How large is ``large enough'' and what does ``as close as we please'' mean? Archimedes and Euclid would not have considered such an argument to be a proof. We will reconsider the end of this proof after we have developed the language to complete it more carefully. (Cf Example 6.54.)
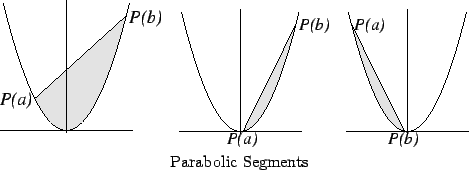
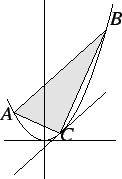
The first person to calculate the area of a parabolic segment was
Archimedes
(287-212 B.C.). The parabolic segment considered by Archimedes corresponds to
the set ![]() bounded by the parabola
bounded by the parabola ![]() and the line joining
and the line joining
![]() to
to
![]() where
where ![]() .
.
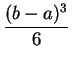 . Use theorem 2.14 and any results from
Euclidean geometry that you need. You may assume that
. Use theorem 2.14 and any results from
Euclidean geometry that you need. You may assume that
The result of this exercise shows that the area of a parabolic segment depends
only on its width. Thus the segment determined by the points ![]() and
and
![]() has the same area as the segment determined by the points
has the same area as the segment determined by the points ![]() and
and
![]() , even though the second segment is 400 times as tall as the
first, and both segments have the same width. Does this seem reasonable?
, even though the second segment is 400 times as tall as the
first, and both segments have the same width. Does this seem reasonable?
Remark: Archimedes
stated his result about the area of a parabolic segment
as follows. The area of the parabolic segment cut off by the
line ![]() is four thirds of the area of the inscribed triangle
is four thirds of the area of the inscribed triangle ![]() , where
, where
![]() is the point on the parabola at which the tangent line is parallel
to
is the point on the parabola at which the tangent line is parallel
to ![]() . We cannot verify Archimedes formula at this time, because we do
not know how to find the point
. We cannot verify Archimedes formula at this time, because we do
not know how to find the point ![]() .
.
The following definition is introduced as a hint for exercise 2.18
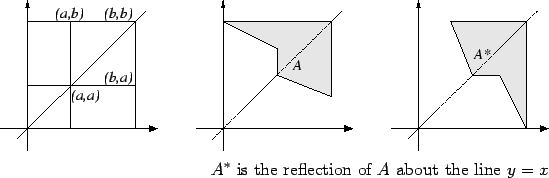
If ![]() denotes the reflection of
denotes the reflection of ![]() about the line
about the line
![]() , then
, then ![]() and
and ![]() have the same area.
have the same area.