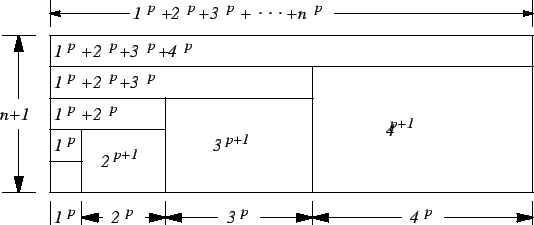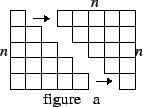
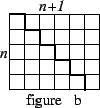
Figure (a) shows two polygons, each having area ![]() . If we slide
the
two polygons so that they touch, we create a rectangle as in figure (b) whose
area is
. If we slide
the
two polygons so that they touch, we create a rectangle as in figure (b) whose
area is ![]() . Thus
. Thus
The proof just given is quite attractive, and a proof similar to this was probably known to the Pythagoreans in the 6th or 5th centuries B.C. Cf [29, page 30]. The formula itself was known to the Babylonians much earlier than this[45, page 77], but we have no idea how they discovered it.
The
idea here is special, and does not generalize to give a formula for
![]() .
(A nice geometrical proof of the formula for the sum of the
first
.
(A nice geometrical proof of the formula for the sum of the
first ![]() squares can be found
in Proofs Without Words by Roger Nelsen[37, page 77],
but it is different enough from the one just given that I would not
call it a ``generalization''.)
We will now give a second proof of (2.8)
that
generalizes to give formulas for
squares can be found
in Proofs Without Words by Roger Nelsen[37, page 77],
but it is different enough from the one just given that I would not
call it a ``generalization''.)
We will now give a second proof of (2.8)
that
generalizes to give formulas for
![]() for positive integers
for positive integers
![]() .
The idea we use was introduced by Blaise
Pascal [6, page 197]
circa 1654.
.
The idea we use was introduced by Blaise
Pascal [6, page 197]
circa 1654.
For any real number ![]() , we have
, we have
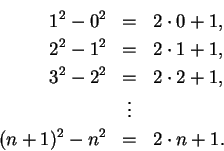
To find
![]() we use the same sort of argument. For any real
number
we use the same sort of argument. For any real
number ![]() we have
we have
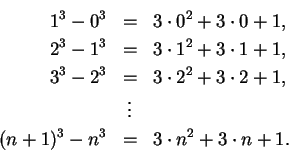
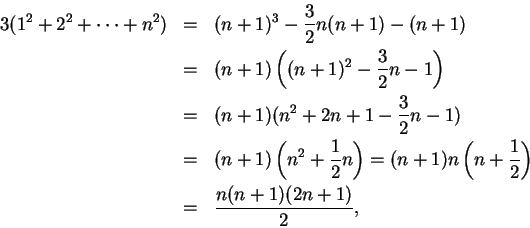
Jacob Bernoulli (1654-1705) considered the
general formula for power sums. By using a technique similar to, but slightly
different from Pascal's, he constructed the table below.
Here
![]() is denoted by
is denoted by ![]() , and
, and ![]() denotes a missing term: Thus
the
denotes a missing term: Thus
the ![]() in the fourth line of the table below indicates that
there is no
in the fourth line of the table below indicates that
there is no ![]() term,
i.e. the coefficient of
term,
i.e. the coefficient of ![]() is zero.
is zero.
Thus we can step by step reach higher and higher powers and with slight effort form the following table.
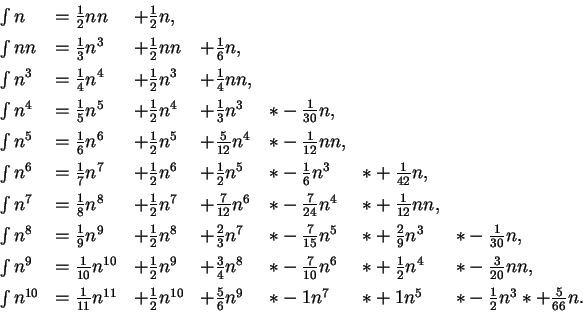
Whoever will examine the series as to their regularity may be able to continue the table[9, pages 317-320]. 2.1
He then states a rule for continuing the table. The rule is not quite an explicit formula, rather it tells how to compute the next line easily when the previous lines are known.
A formula for
![]() was proved by Archimedes (287-212 B.C.).
(See Archimedes On Conoids and Spheroids in [2, pages
107-109]).
The formula was known to the Babylonians[45, page 77]
much earlier than this in the form
was proved by Archimedes (287-212 B.C.).
(See Archimedes On Conoids and Spheroids in [2, pages
107-109]).
The formula was known to the Babylonians[45, page 77]
much earlier than this in the form
A technique for calculating general power sums has been known since circa
1000 A.D. At about this time
Ibn-al-Haitham, gave a method based on the picture
below, and used it to calculate the power sums up to
![]() . The method is discussed in [6, pages 66-69]
. The method is discussed in [6, pages 66-69]