From now on I will denote points in the plane by lower case boldface letters,
e.g.
![]() . If I specify a point
. If I specify a point
![]() and do not explicitly write
down its
components, you should assume
and do not explicitly write
down its
components, you should assume
![]() , etc. The one exception to this rule is that I will always
take
, etc. The one exception to this rule is that I will always
take
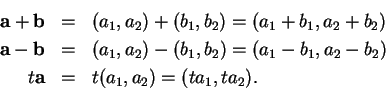
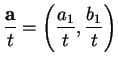 . We will
abbreviate
. We will
abbreviate
We have the following law that resembles the associative law for
multiplication:
We have the following distributive laws:
All of these properties follow easily from the corresponding properties of real numbers. I will prove the commutative law and one of the distributive laws, and omit the remaining proofs.
Proof of Commutative Law: Let
![]() be points in
be points in
![]() .
By
the commutative law for
.
By
the commutative law for
![]() ,
,
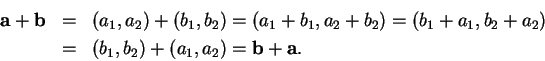
Proof of (4.3): Let
![]() and let
and let
![]() . By
the
distributive law for
. By
the
distributive law for
![]() we have
we have
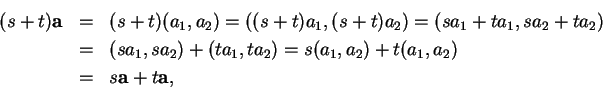
Remark: Let
![]() ,
,
![]() be points in
be points in
![]() such that
such that
![]() and
and
![]() are not all in a straight line. Then
are not all in a straight line. Then
![]() is the vertex opposite
is the vertex opposite
![]() in the parallelogram whose other three vertices are
in the parallelogram whose other three vertices are
![]() and
and
![]() .
.
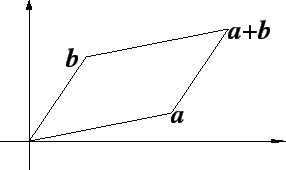
Proof: In this proof I will suppose ![]() and
and ![]() , so
that neither of
, so
that neither of
![]() is a vertical line. (I leave the other cases
to you.)
The slope of line
is a vertical line. (I leave the other cases
to you.)
The slope of line
![]() is
is
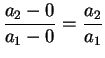 , and the slope of
, and the slope of
![]() is
is
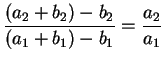 . Thus the lines
. Thus the lines
![]() and
and
![]() are parallel.
are parallel.
The slope of line
![]() is
is
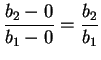 ,
and
the slope of
,
and
the slope of
![]() is
is
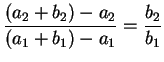 . Thus the lines
. Thus the lines
![]() and
and
![]() are parallel. It follows that the figure
are parallel. It follows that the figure
![]() is a
parallelogram,
i.e.,
is a
parallelogram,
i.e.,
![]() is the fourth vertex of a parallelogram having
is the fourth vertex of a parallelogram having
![]() and
and
![]() as its other vertices.
as its other vertices. ![]()
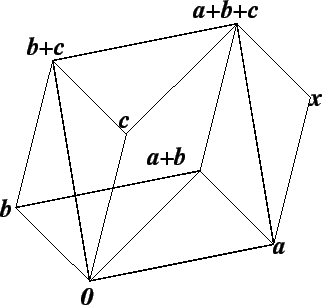
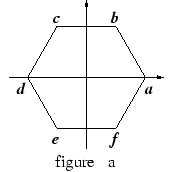
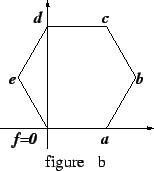
In figure b),
![]() and
and
![]() are the vertices of a
regular
hexagon with
are the vertices of a
regular
hexagon with
![]() . Sketch the points
. Sketch the points
![]() , and
, and
![]() as accurately as you can.
(This
problem should be done geometrically. Do not calculate the coordinates of any
of
these points.)
as accurately as you can.
(This
problem should be done geometrically. Do not calculate the coordinates of any
of
these points.)
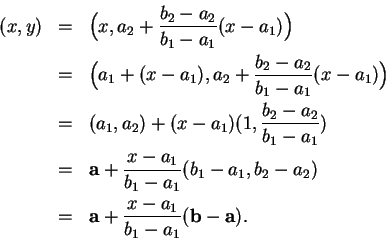
![\begin{eqnarray*}
x \in [a_1,b_1] &\mbox{$\Longleftrightarrow$}& a_1 \leq x \le...
...x{$\Longleftrightarrow$}& 0 \leq {x-a_1 \over b_1 - a_1} \leq 1.
\end{eqnarray*}](img904.gif)
![\begin{eqnarray*}[\mbox{{\bf a}}\mbox{{\bf b}}]&=& [\mbox{{\bf b}}\mbox{{\bf a}}...
...f a}}+ (1-t)(\mbox{{\bf b}}- \mbox{{\bf a}}): 0 \leq t \leq 1\}.
\end{eqnarray*}](img907.gif)