


Next: Some General Remarks
Up: Introduction
Previous: Remembrance of Things Past
Index
In this course we will reorganize all of the number facts with which
you are familiar. We will make a small number of assumptions or
axioms
about
numbers, (thirteen assumptions in all, in definitions (2.48),
(2.100), and (5.21)). The first twelve assumptions
will be familiar number facts. The last assumption may not
look familiar, but I hope it will seem as plausible as
things you have assumed about numbers in the past.
You will not be permitted to assume any facts about numbers
other than the thirteen stated assumptions. For example,
we will not assume that 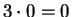 , or that
, or that 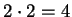 ,
so you will not be allowed to assume this. (These facts
will be proved in theorems 2.66 and 2.84.)
You will not be allowed to assume that
,
so you will not be allowed to assume this. (These facts
will be proved in theorems 2.66 and 2.84.)
You will not be allowed to assume that
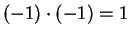 , or that
, or that
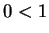 . (These facts will follow from exercise
2.77c
and corollary 2.104.)
We will not justify the representation of numbers
by points on a line, so no proofs can depend on pictures
of graphs of functions.
On the basis of our assumptions about real numbers, we will construct
a more general class of complex numbers, in which
. (These facts will follow from exercise
2.77c
and corollary 2.104.)
We will not justify the representation of numbers
by points on a line, so no proofs can depend on pictures
of graphs of functions.
On the basis of our assumptions about real numbers, we will construct
a more general class of complex numbers, in which 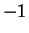 , and in
fact every number, has a square root. Many results about the algebra
and calculus of real functions will be shown to hold for complex
functions.
, and in
fact every number, has a square root. Many results about the algebra
and calculus of real functions will be shown to hold for complex
functions.
Occasionally I will draw pictures
to motivate proofs, but the proofs themselves will not
depend on the pictures.
The goal of the course is to ``contemplate the very nature of numbers
by thought alone, practising it not for the purpose of
buying and selling like merchants and hucksters, but  to
make easier the change from the world of becoming to real
being and truth.''
to
make easier the change from the world of becoming to real
being and truth.''
Sometimes in examples or remarks I will use arguments
depending on similar triangles or trigonometric identities,
but my theorems and definitions will depend only
on my assumptions. I will also refer to integers and rational
numbers in examples before I give the formal definitions,
but no theorems will involve integers until they have been defined.
Nothing in this course will be trivial or obvious or clear.
If you come across these words, it probably means that I am
engaging in a mild deception. Beware.
In theorem 2.66 we will prove the well known
fact that 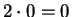 . In
(12.57),
we will prove the less well known fact that
. In
(12.57),
we will prove the less well known fact that
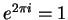 .
The fact that we can derive the last not-so-obvious result
from our thirteen assumptions is somewhat remarkable.
.
The fact that we can derive the last not-so-obvious result
from our thirteen assumptions is somewhat remarkable.



Next: Some General Remarks
Up: Introduction
Previous: Remembrance of Things Past
Index
![]() to
make easier the change from the world of becoming to real
being and truth.''
to
make easier the change from the world of becoming to real
being and truth.''
![]() . In
(12.57),
we will prove the less well known fact that
. In
(12.57),
we will prove the less well known fact that
![]() .
The fact that we can derive the last not-so-obvious result
from our thirteen assumptions is somewhat remarkable.
.
The fact that we can derive the last not-so-obvious result
from our thirteen assumptions is somewhat remarkable.