


Next: The Goal of the
Up: Introduction
Previous: Introduction
Index
You have been working with numbers for most of your life,
and you know hundreds of facts about them. The first numbers you encountered
were probably the positive integers 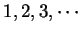 . You learned that
multiplication was repeated addition, and that
. You learned that
multiplication was repeated addition, and that
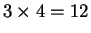 , because
3 groups of apples, each of which contains 4 apples combine to
give a group of 12 apples. Later you learned that
, because
3 groups of apples, each of which contains 4 apples combine to
give a group of 12 apples. Later you learned that
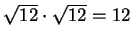 . This did not mean that
. This did not mean that 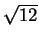 groups of apples,
each of which contained
groups of apples,
each of which contained 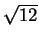 apples combine to give a group
of
apples combine to give a group
of 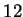 apples. The definition had changed, but
whatever it meant, you knew how to get the ``right answer''. At some point
you met decimals.
Since
apples. The definition had changed, but
whatever it meant, you knew how to get the ``right answer''. At some point
you met decimals.
Since
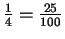 , you knew
that
, you knew
that
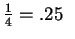 .
.
However 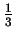 was more of
a problem. Although
was more of
a problem. Although 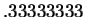 was close to
was close to 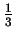 , the two
numbers were not equal. Perhaps you considered infinite decimals,
so
, the two
numbers were not equal. Perhaps you considered infinite decimals,
so
Then
But
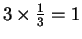 , So
, So
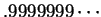 must be equal to
must be equal to 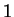 .
They don't look equal, but
.
They don't look equal, but 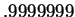 was probably close enough.
At first the fact that
was probably close enough.
At first the fact that
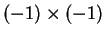
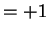 was probably rather puzzling,
but you got used to it after a while.
You may have encountered the imaginary number
was probably rather puzzling,
but you got used to it after a while.
You may have encountered the imaginary number 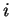 such that
such that 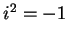 and
and
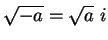 when
when 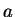 is positive. Then you found that
is positive. Then you found that
and
This may have been unnerving.
At some time numbers became identified with points on a line.
Addition is straightforward: to add two numbers, you just
slide the lines so that they share a common end, and combine them into
one line.
but what does multiplication mean?



Next: The Goal of the
Up: Introduction
Previous: Introduction
Index