



Next: 5.3 Existence of Roots
Up: 5. Real Numbers
Previous: 5.1 Sequences and Search
Index
5.21
Definition (Completeness axiom.)
Let

be an ordered field.
We say that

is
complete if it satisfies
the condition:
Every binary
search sequence in  converges to a unique point in
converges to a unique point in  .
.
5.22
Example.
The field
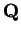
is not complete, since in example
5.16 we found a
binary search sequence in
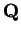
that does not converge.
5.23
Definition (Real field,
 .)
.)
A
real field is a complete
ordered field. We will use the name

to denote
a real field.
5.24
Remark.
It is not at all clear that any real fields exist. If real fields do exist, there is
a question of uniqueness;
i.e., is it the case that any two real fields are ``essentially the same"? I don't want to worry about what mathematical existence
means, so let me formulate the questions: Are the axioms for a real field
consistent; i.e., is it the case that no contradictions can be derived from them?
Note that we are not entirely free to throw axioms together. If I were to make a
definition that a
3-field is an ordered field in which
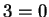
, I would
immediately get a contradiction:
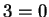
and
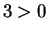
. All I can say about consistency is
that no contradictions have been found to follow from the real field axioms. There
exist proofs that any two real fields are essentially the same, cf. [
35, page
129]. (This source uses a different statement for the completeness axiom
than we have used, but the axiom system is equivalent to ours.) There also exist
constructions of pairs of very different real fields, cf. [
41].
In what follows, I am going to assume that there is a real field
 (which I'll
call the real numbers). Any theorems proved will be valid in all real fields.
(which I'll
call the real numbers). Any theorems proved will be valid in all real fields.
5.25
Theorem (Archimedean property 1.)
Let
 be a real field, and let
be a real field, and let
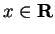 . Then there is an integer
. Then there is an integer
 such that
such that 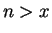 .
.
Proof: Let
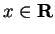 , and suppose (in order to get a contradiction) that there is no
, and suppose (in order to get a contradiction) that there is no
 with
with 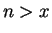 . Then
. Then 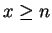 for all
for all  . Now
. Now
![$\displaystyle { \left\{ \left[
0,{x\over {2^n}}\right]\right\}}$](img1341.gif) is a binary search sequence in
is a binary search sequence in
 . Since
. Since 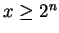 , I have
, I have
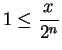 for all
for all
 . We see that
. We see that
![$\displaystyle {
\left\{\left[ 0,{x\over {2^n}}\right]\right\}\to 1}$](img1344.gif) , but clearly
, but clearly
![$\displaystyle {
\left\{\left[ 0,{x\over {2^n}}\right]\right\}\to 0}$](img1345.gif) . Since completeness of
. Since completeness of
 implies that a binary search sequence has a unique limit, this yields a
contradiction, and proves the theorem.
implies that a binary search sequence has a unique limit, this yields a
contradiction, and proves the theorem.
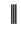
5.26
Corollary (Archimedean property 2.)
Let
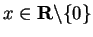 . Then there is some
. Then there is some
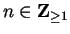 such that
such that
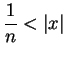 .
.
Proof: By the theorem, there is some
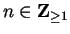 with
with
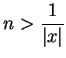 . Then
. Then
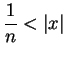 .
.

Proof: Let
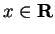 , and let
, and let
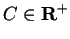 satisfy
satisfy
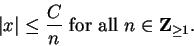 |
(5.29) |
Suppose, in order to get a contradiction, that 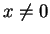 . Then
by Archimedian property 2 there is some
. Then
by Archimedian property 2 there is some
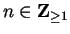 such that
such that
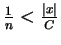 , i.e.
, i.e.
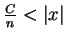 .
This contradicts (5.29).
.
This contradicts (5.29).

5.30
Theorem.
If
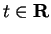 , then there is
an integer
, then there is
an integer  and a number
and a number
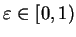 such that
such that
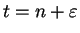 .
.
In order to prove this theorem, I will use the following lemma.
5.31
Lemma.
If
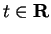 , then the interval
, then the interval ![$(t,t+1]$](img1356.gif) contains an integer.
contains an integer.
Proof:
- Case 1.
-
 : Suppose
: Suppose
 and
and ![$(t,t+1]$](img1356.gif) does not
contain an integer. I will show that
does not
contain an integer. I will show that 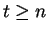 for all
for all
 . This contradicts the
Archimedean property, so no such
. This contradicts the
Archimedean property, so no such 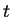 can exist. For each
can exist. For each
 , let
, let
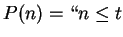 ". Then
". Then 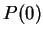 is true, since I assumed that
is true, since I assumed that
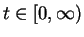 . Let
. Let
 be a number such that
be a number such that 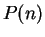 is true; i.e.,
is true; i.e., 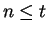 . If
. If 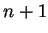 were
were 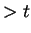 ,
we'd have
,
we'd have 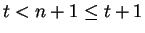 , and this cannot happen, since
, and this cannot happen, since ![$(t,t+1]$](img1356.gif) contains no
integers. Hence,
contains no
integers. Hence,
and by induction, 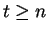 for all
for all
 . This gives the desired contradiction.
. This gives the desired contradiction.
- Case 2.
-
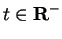 : If
: If
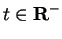 , then by Case 1 there is an integer
, then by Case 1 there is an integer  with
with
Then
If 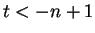 , then
, then ![$(t,t+1]$](img1356.gif) contains
contains 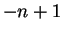 . If
. If 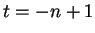 , then
, then
![$(t,t+1]=(-n+1,-n+2]$](img1371.gif) contains
contains 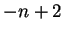 .
.

Proof of theorem 5.30. Let
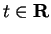 . By the lemma, there is an integer
. By the lemma, there is an integer
 with
with 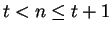 . Then
. Then
and
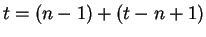 gives the desired decomposition.
gives the desired decomposition.

5.32
Theorem.
There is a number
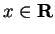 such that
such that 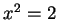 .
.
Proof: Let ![$\{[a_n,b_n]\}$](img1289.gif) be the binary search sequence constructed in example
5.16. We know there is a unique
be the binary search sequence constructed in example
5.16. We know there is a unique
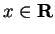 such that
such that
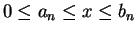 for all
for all  . Then
. Then
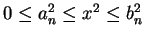 , and by our construction
, and by our construction
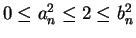 for all
for all
 , so
, so
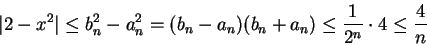 |
(5.33) |
for all
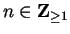 .
.
By Archimedean property 3, we conclude that
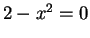 , i.e.,
, i.e., 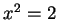 .
.

5.34
Theorem.
Let
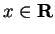 . Then there is a binary search sequence
. Then there is a binary search sequence ![$\{[a_n,b_n]\}$](img1289.gif) in
in
 such
that
such
that
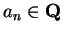 and
and
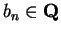 for all
for all  , and such that
, and such that
![$\{[a_n,b_n]\}\to x$](img1294.gif) .
.
Proof: I will suppose 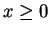 . The case where
. The case where 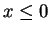 is left to you. By the
Archimedean property of
is left to you. By the
Archimedean property of
 , there is an integer
, there is an integer 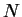 such that
such that 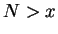 , so
, so
![$x\in[0,N]$](img1387.gif) . Now build a binary search sequence
. Now build a binary search sequence ![$\{[a_n,b_n]\}$](img1289.gif) as follows:
as follows:
From the construction, we have
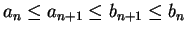 and
and
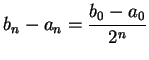 .
A simple induction argument shows that
.
A simple induction argument shows that
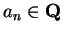 and
and
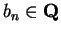 for all
for all
 ,
and an induction proof similar to the one in
example 5.16 shows that
,
and an induction proof similar to the one in
example 5.16 shows that
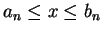 for all
for all
 so
so
![$\{[a_n,b_n]\}\to x$](img1294.gif) .
.





Next: 5.3 Existence of Roots
Up: 5. Real Numbers
Previous: 5.1 Sequences and Search
Index
![]() converges to a unique point in
converges to a unique point in ![]() .
.
![]() converges to a unique point in
converges to a unique point in ![]() .
.
![]() (which I'll
call the real numbers). Any theorems proved will be valid in all real fields.
(which I'll
call the real numbers). Any theorems proved will be valid in all real fields.
![]() , and suppose (in order to get a contradiction) that there is no
, and suppose (in order to get a contradiction) that there is no
![]() with
with ![]() . Then
. Then ![]() for all
for all ![]() . Now
. Now
![$\displaystyle { \left\{ \left[
0,{x\over {2^n}}\right]\right\}}$](img1341.gif) is a binary search sequence in
is a binary search sequence in
![]() . Since
. Since ![]() , I have
, I have
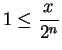 for all
for all
![]() . We see that
. We see that
![$\displaystyle {
\left\{\left[ 0,{x\over {2^n}}\right]\right\}\to 1}$](img1344.gif) , but clearly
, but clearly
![$\displaystyle {
\left\{\left[ 0,{x\over {2^n}}\right]\right\}\to 0}$](img1345.gif) . Since completeness of
. Since completeness of
![]() implies that a binary search sequence has a unique limit, this yields a
contradiction, and proves the theorem.
implies that a binary search sequence has a unique limit, this yields a
contradiction, and proves the theorem.
![]()
![]() with
with
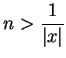 . Then
. Then
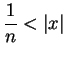 .
.
![]()
![]() . By the lemma, there is an integer
. By the lemma, there is an integer
![]() with
with ![]() . Then
. Then
![]() be the binary search sequence constructed in example
5.16. We know there is a unique
be the binary search sequence constructed in example
5.16. We know there is a unique
![]() such that
such that
![]() for all
for all ![]() . Then
. Then
![]() , and by our construction
, and by our construction
![]() for all
for all
![]() , so
, so
![]() , i.e.,
, i.e., ![]() .
.
![]()
![]() . The case where
. The case where ![]() is left to you. By the
Archimedean property of
is left to you. By the
Archimedean property of
![]() , there is an integer
, there is an integer ![]() such that
such that ![]() , so
, so
![]() . Now build a binary search sequence
. Now build a binary search sequence ![]() as follows:
as follows:
![\begin{eqnarray*}[a_0,b_0]&=&[0,N] \cr
[a_{n+1},b_{n+1}]&=&\cases{ \left[a_n, {{...
...over 2},b_n\right] &if $x>\left[ {{a_n+b_n}\over 2}\right]$.\cr}
\end{eqnarray*}](img1388.gif)
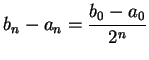 .
A simple induction argument shows that
.
A simple induction argument shows that