We will now give an example of a function ![]() that is continuous at every point
of
that is continuous at every point
of
![]() and differentiable at no point of
and differentiable at no point of ![]() . The first published example
of
such a function appeared in 1874 and was due to Karl Weierstrass(1815-1897)
[29, page 976].
The example described below is due to Helga von Koch (1870-1924),
and is a slightly modified version of Koch's snowflake. From the
discussion in section 2.6, it is not really clear what we would
mean by
the perimeter of a snowflake, but it is pretty clear that whatever the
perimeter might be, it is not the graph of a function. However, a slight
modification of Koch's construction yields an everywhere continuous but nowhere
differentiable function.
. The first published example
of
such a function appeared in 1874 and was due to Karl Weierstrass(1815-1897)
[29, page 976].
The example described below is due to Helga von Koch (1870-1924),
and is a slightly modified version of Koch's snowflake. From the
discussion in section 2.6, it is not really clear what we would
mean by
the perimeter of a snowflake, but it is pretty clear that whatever the
perimeter might be, it is not the graph of a function. However, a slight
modification of Koch's construction yields an everywhere continuous but nowhere
differentiable function.
We will construct a sequence ![]() of functions on
of functions on ![]() . The graph of
. The graph of
![]() will be a polygonal line with
will be a polygonal line with ![]() segments. We set
segments. We set
In general
the graph of ![]() is obtained from the graph of
is obtained from the graph of ![]() by replacing each
segment
by replacing each
segment
![]() in the graph of
in the graph of ![]() by four segments
by four segments
![]() and
and
![]() constructed according to the following three rules:
constructed according to the following three rules:
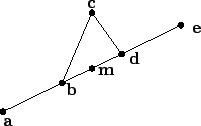
 .
.
The function ![]() provides us with an example of a continuous function that is
not
piecewise monotonic over any interval.
provides us with an example of a continuous function that is
not
piecewise monotonic over any interval.