



Next: 12.2 A Nowhere Differentiable
Up: 12. Extreme Values of
Previous: 12. Extreme Values of
Index
12.1
Definition (Continuity at a point.)
Let

be a real valued function such that
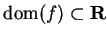
. Let
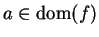
. We say that
 is continuous at
is continuous at 
if and only if
Remark: According to this definition, in order for  to be continuous at
to be continuous at
 we
must have
we
must have
and
The second condition is often not included in the definition of continuity, so
this
definition does not quite correspond to the usual definition.
Remark: The method we will usually use to show that
a function  is not continuous at a point
is not continuous at a point  , is to find a
sequence
, is to find a
sequence 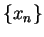 in
in
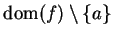 such that
such that
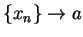 , but
, but 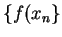 either diverges or converges
to a value different from
either diverges or converges
to a value different from 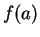 .
.
12.2
Definition (Continuity on a set.)
Let

be a real valued function such that
domain
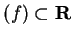
, and let

be a subset of domain
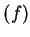
.
We say that
 is continuous on
is continuous on 
if

is continuous at
every point in

. We say that
 is continuous
is continuous if

is
continuous at every point of domain
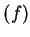
.
12.3
Example (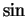 ,
, 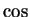 ,
, 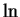 and power functions are continuous.)
and power functions are continuous.)
We
proved in lemma
11.17 that a function is continuous at every point
at
which it is differentiable. (You should now check the proof of that lemma to
see
that we did prove this.) Hence
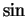
,
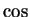
,
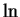
, and
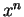
(for
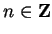
) are all
continuous on their domains, and if
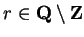
, then
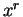
is
continuous on
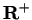
.
12.4
Example.
Let
Then

is not continuous at
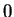
. For the sequence
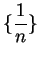
converges to
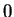
, but
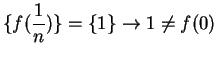
.
Our limit rules all give rise to theorems
about continuous functions.
12.5
Theorem (Properties of continuous functions.) Let 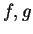 be real valued functions with
be real valued functions with
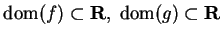 ,
and let
,
and let
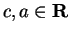 . If
. If  and
and  are continuous at
are continuous at  and if
and if  is
approachable from
is
approachable from
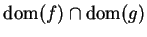 , then
, then
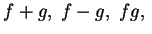 and
and 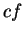 are
continuous
at
are
continuous
at  . If in addition,
. If in addition, 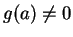 then
then
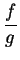 is also continuous
at
is also continuous
at  .
.
Proof: Suppose  and
and  are continuous at
are continuous at  , and
, and  is approachable from
is approachable from
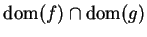 . Then
. Then
By the sum rule for limits (theorem 10.15) it follows that
Thus 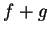 is continuous at
is continuous at  . The proofs of the other parts
of the theorem are similar.
. The proofs of the other parts
of the theorem are similar.
12.6
Example (An everywhere discontinuous function.)
Let
be the example of a non-integrable function defined in equation
(
8.37). Then
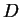
is not continuous at any point of
![$[0,1]$](img908.gif)
. Recall
where

is a subset of
![$[0,1]$](img908.gif)
such that every subinterval of
![$[0,1]$](img908.gif)
of
positive
length contains a point in

and a point not in

. Let
![$x\in [0,1]$](img2197.gif)
.
- Case 1.
- If
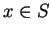 we can find a sequence of points
we can find a sequence of points 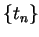 in
in
![$[0,1]\setminus S$](img3129.gif) such that
such that 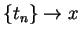 . Then
. Then
so 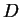 is not continuous at
is not continuous at  .
.
- Case 2.
- If
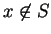 we can find a sequence of points
we can find a sequence of points 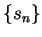 in
in  such
that
such
that 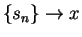 . Then
. Then
so 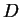 is not continuous at
is not continuous at  .
.
12.7
Example.
Let
I claim that
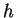
is continuous. We know that
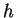
is differentiable on
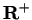
,
so
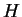
is continuous at each point of
. In example
10.13 we
showed
that
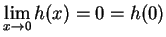
so
is also continuous at
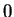
.
12.8
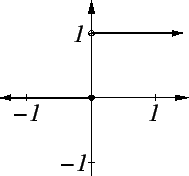
Example.
Let
Then

and

are both continuous functions. Now
and hence
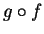
is not continuous. The domain of
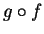
contains just
one
point, and that point is not approachable from
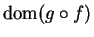
.
Proof: Suppose  is continuous at
is continuous at  and
and  is continuous at
is continuous at 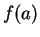 , and
, and
 is
approachable from
is
approachable from
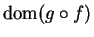 . Let
. Let 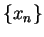 be a
sequence in
be a
sequence in
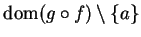 such
that
such
that 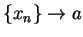 . Then
. Then
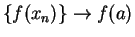 since
since  is continuous at
is continuous at  .
Hence
.
Hence
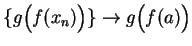 since
since  is continuous at
is continuous at 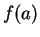 ;
i.e.,
;
i.e.,
Hence 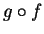 is continuous
at
is continuous
at
 .
.




Next: 12.2 A Nowhere Differentiable
Up: 12. Extreme Values of
Previous: 12. Extreme Values of
Index
Ray Mayer
2007-09-07
![]() to be continuous at
to be continuous at
![]() we
must have
we
must have
![]() is not continuous at a point
is not continuous at a point ![]() , is to find a
sequence
, is to find a
sequence ![]() in
in
![]() such that
such that
![]() , but
, but ![]() either diverges or converges
to a value different from
either diverges or converges
to a value different from ![]() .
.
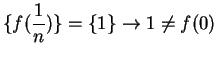 .
.
![]() and
and ![]() are continuous at
are continuous at ![]() , and
, and ![]() is approachable from
is approachable from
![]() . Then
. Then
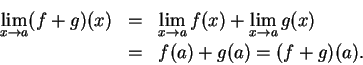
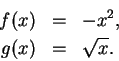
![]() is continuous at
is continuous at ![]() and
and ![]() is continuous at
is continuous at ![]() , and
, and
![]() is
approachable from
is
approachable from
![]() . Let
. Let ![]() be a
sequence in
be a
sequence in
![]() such
that
such
that ![]() . Then
. Then
![]() since
since ![]() is continuous at
is continuous at ![]() .
Hence
.
Hence
![]() since
since ![]() is continuous at
is continuous at ![]() ;
i.e.,
;
i.e.,