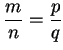 where
where
Proof: Since ![]() we can choose an odd integer
we can choose an odd integer ![]() such that
such that
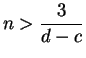 , i.e.,
, i.e., ![]() . Since the interval
. Since the interval ![]() has length
has length
![]() , it
contains at least two integers
, it
contains at least two integers ![]() , say
, say ![]() . If
. If ![]() and
and ![]() are both
odd, then there is an even integer between them, and if
are both
odd, then there is an even integer between them, and if ![]() and
and ![]() are both
even,
there is an odd integer between them, so in all cases we can find a set of
integers
are both
even,
there is an odd integer between them, so in all cases we can find a set of
integers
![]() one of which is even and the other is odd such that
one of which is even and the other is odd such that ![]() ,
i.e.,
,
i.e.,
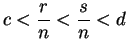 . Then
. Then
![]() and
and
![]() are
two elements of
are
two elements of ![]() one of which
is in
one of which
is in ![]() , and the other of which is in
, and the other of which is in ![]() .
. ![]()
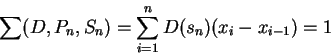
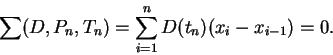
Our example of a non-integrable function is a slightly modified version of an example given by P. G. Lejeune Dirichlet (1805-1859) in 1837. Dirichlet's example was not presented as an example of a non-integrable function (since the definition of integrability in our sense had not yet been given), but rather as an example of how badly behaved a function can be. Before Dirichlet, functions that were this pathological had not been thought of as being functions. It was examples like this that motivated Riemann to define precisely what class of functions are well enough behaved so that we can prove things about them.