8.38
Example (Ruler function.)
We now present an example of an integrable function
that
is not monotonic on any interval of positive length. Define
![$R:[0,1]\to\mbox{{\bf R}}$](img2169.gif)
by
This formula defines
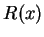
uniquely: If
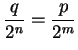
where
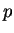
and
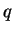
are odd, then
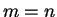
. (If
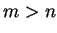
, we get
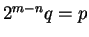
,
which says
that an even number is odd.) The set
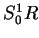
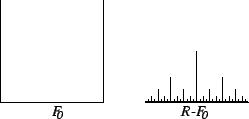
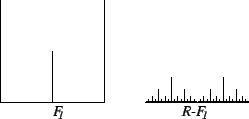
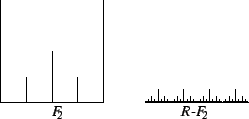
under the graph of
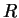
is shown
in
the figure.
This set resembles the markings giving fractions of an inch on a
ruler, which motivates the name
ruler function for
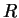
.
It is easy to see that
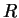
is not monotonic on any interval of length
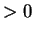
.
For each
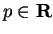
let
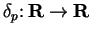
be defined by
We have seen that
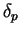
is integrable on any interval
![$[a,b]$](img1071.gif)
and
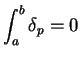
. Now define a sequence of functions
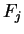
by
Each function
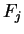
is integrable with integral
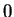
and
I will now show that 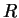 is integrable.
is integrable.
Let
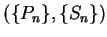 be a partition-sample sequence for
be a partition-sample sequence for ![$[0,1]$](img908.gif) . I'll show
that
. I'll show
that
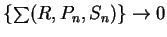 .
.
Let 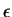 be a generic element in
be a generic element in
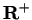 .
Observe that if
.
Observe that if
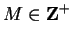 then
then
Hence by the Archimedian property, we can
choose
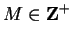
so that
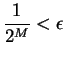
. Then
Now since
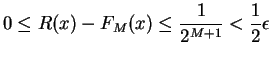
for
all
![$x\in [0,1]$](img2197.gif)
, we have
Since
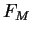
is integrable and
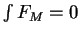
, we have
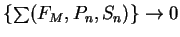
so there is an
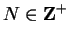
such that
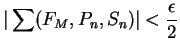
for all
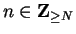
. By equation (
8.40) we have
Hence
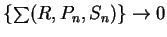
, and hence
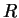
is integrable and
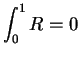
.
8.41
Exercise.
A
Let
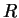
be the ruler function. We just gave a complicated proof that
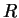
is
integrable and
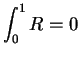
. Explain why if you
assume 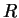
is
integrable, then it is easy to show that
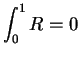
.
Also show that
if you assume that the non-integrable function 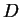 in equation (8.37)
is integrable then it
is easy
to show that
in equation (8.37)
is integrable then it
is easy
to show that
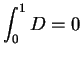 .
.
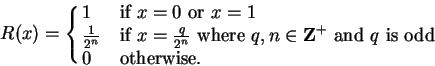
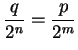 where
where 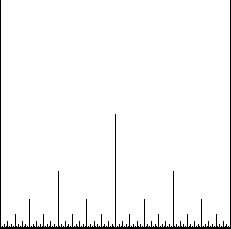
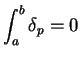 . Now define a sequence of functions
. Now define a sequence of functions 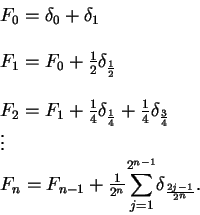
![]() is integrable.
is integrable.
![]() be a partition-sample sequence for
be a partition-sample sequence for ![]() . I'll show
that
. I'll show
that
![]() .
.
![]() be a generic element in
be a generic element in
![]() .
Observe that if
.
Observe that if
![]() then
then
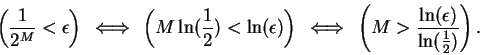
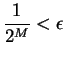 . Then
. Then
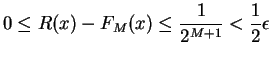 for
all
for
all 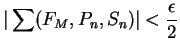 for all
for all
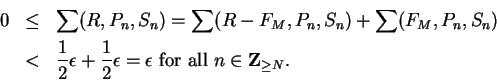
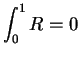 .
.
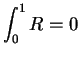 . Explain why if you assume
. Explain why if you assume 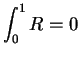 .
.
![]() in equation (8.37)
is integrable then it
is easy
to show that
in equation (8.37)
is integrable then it
is easy
to show that
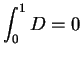 .
.