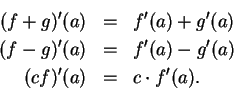
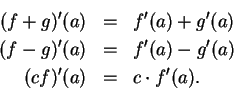
Proof: We will prove only the first statement. The proofs of the
other statements are similar. For all
![]() we have
we have
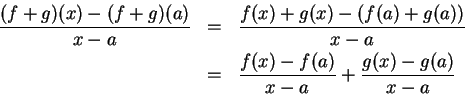
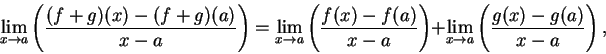
If
![]() , then
, then
![]() , so
, so
If
![]() , then
, then
 , so
, so
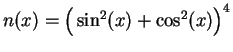
Proof:
Let ![]() be a generic point of
be a generic point of
![]() . Then
. Then
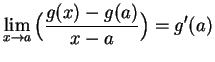 and
and
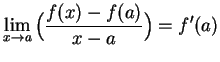 .
If we
also knew that
.
If we
also knew that
This missing result will be needed in some other theorems, so I've isolated it in the following lemma.
Proof:
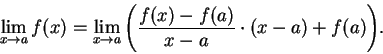
is the difference between two successive
's; let one of these be
and the other
into
; then we have
the omission of the quantityNotice that for Leibniz, the important thing is not the derivative,which is infinitely small in comparison with the rest, for it is supposed that
and
are infinitely small (because the lines are understood to be continuously increasing or decreasing by very small increments throughout the series of terms), will leave
.[34, page 143]
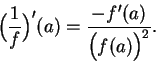
Proof: For all
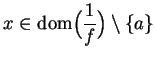
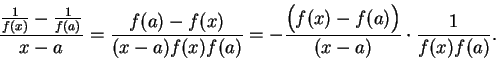
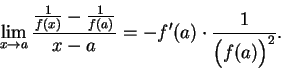
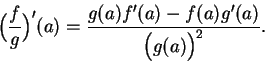
Let
![]() . Then by the product rule
. Then by the product rule
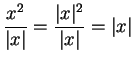 ).
).
The calculation is not valid at ![]() (since
(since ![]() is not differentiable
at
is not differentiable
at ![]() , and we divided by
, and we divided by ![]() in the calculation. However
in the calculation. However ![]() is differentiable
at
is differentiable
at ![]() since
since
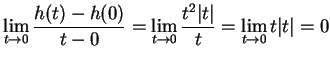 , i.e.,
, i.e.,
![]() . Hence the
formula
. Hence the
formula
Let
![]() . Consider
. Consider ![]() to be a product
to be a product
![]() where
where
![]() and
and ![]() . Then we can apply the
product rule twice to get
. Then we can apply the
product rule twice to get
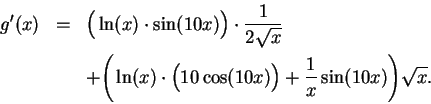
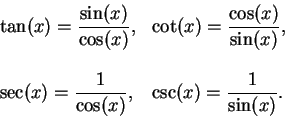
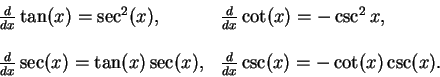
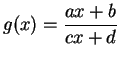 (here
(here 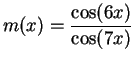 .
.
a) Express ![]() in terms of
in terms of ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
b) On the basis of your answer for part a), try to guess
a formula for ![]() . Then calculate
. Then calculate ![]() , and see whether
your guess was right.
, and see whether
your guess was right.