



Next: 9.2 Calculation of
Up: 9. Trigonometric Functions
Previous: 9. Trigonometric Functions
Index
9.1
Definition (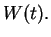 )
)
We define a function
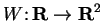
as follows.
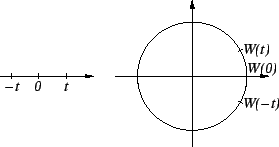
If 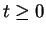 , then
, then 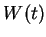 is the point on the unit circle such that the length
of
the arc joining
is the point on the unit circle such that the length
of
the arc joining 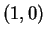 to
to 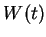 (measured in the counterclockwise direction)
is
equal to
(measured in the counterclockwise direction)
is
equal to  . (There is an optical illusion
in the figure. The length of segment
. (There is an optical illusion
in the figure. The length of segment ![$[0,t]$](img2300.gif) is equal to the length of
arc
is equal to the length of
arc 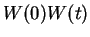 .)
.)
Thus to find
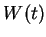
, you should start at
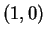
and move along
the
circle in a counterclockwise direction until you've traveled a distance

.
Since the circumference of the circle is
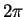
, we see that
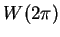
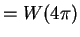
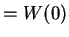
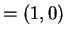
.
(Here we assume Archimedes'
result that the area
of a circle is half the circumference times the radius.)
If
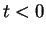
, we define
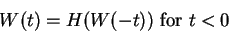 |
(9.2) |
where
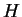
is the reflection about the horizontal axis. Thus if
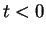
, then
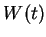
is
the
point obtained by starting at
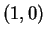
and moving
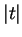
along the unit circle in
the
clockwise direction.
Remark: The definition of 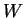 depends on several ideas that we have not
defined
or stated assumptions about, e.g., length of an arc and
counterclockwise
direction. I believe that the amount of work it takes to formalize these
ideas at this
point is not worth the effort, so I hope your geometrical intuition will carry
you
through this chapter. (In this chapter we will assume quite a bit
of Euclidean geometry, and a few properties of area that
do not follow from our assumptions stated in chapter 5.)
depends on several ideas that we have not
defined
or stated assumptions about, e.g., length of an arc and
counterclockwise
direction. I believe that the amount of work it takes to formalize these
ideas at this
point is not worth the effort, so I hope your geometrical intuition will carry
you
through this chapter. (In this chapter we will assume quite a bit
of Euclidean geometry, and a few properties of area that
do not follow from our assumptions stated in chapter 5.)
A more self contained treatment of the trigonometric functions
can be found in [44, chapter 15], but the treatment given
there uses ideas that we will consider later, (e.g. derivatives,
inverse functions,
the intermediate value theorem, and the fundamental theorem of calculus)
in order to define the trigonometric functions.
We have the following values for 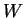 :
:
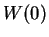 |
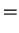 |
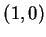 |
(9.3) |
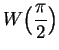 |
 |
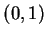 |
(9.4) |
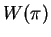 |
 |
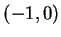 |
(9.5) |
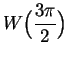 |
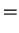 |
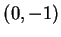 |
(9.6) |
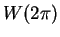 |
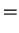 |
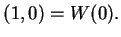 |
(9.7) |
In general
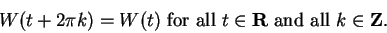 |
(9.8) |
9.9
Definition (Sine and cosine.)
In terms of coordinates, we write
(We read ``
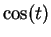
" as `` cosine of

", and we read ``
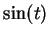
" as
`` sine of

".)
Since 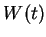 is on the unit circle, we have
is on the unit circle, we have
and
The equations (9.3) - (9.8) show that
and
In equation (9.2) we defined
Thus for 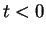 ,
,
and it follows that
In terms of components
and consequently
Let 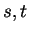 be arbitrary real numbers. Then there exist integers
be arbitrary real numbers. Then there exist integers 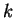 and
and 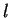 such that
such that
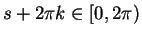 and
and
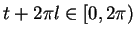 . Let
. Let
Then
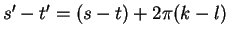 , so
, so
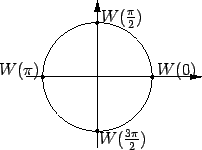
Suppose
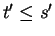 (see figure). Then the length of the arc joining
(see figure). Then the length of the arc joining
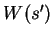 to
to 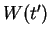 is
is
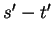 which is the same as the
length of
the arc joining
which is the same as the
length of
the arc joining 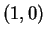 to
to
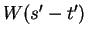 . Since equal arcs in a
circle subtend
equal chords, we have
. Since equal arcs in a
circle subtend
equal chords, we have
and hence
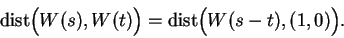 |
(9.10) |
You can verify that this same relation holds when
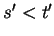 .
.
Proof: From (9.10) we know
i.e.,
Hence
By expanding the squares and using the fact that
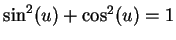 for
all
for
all 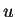 ,
we conclude that
,
we conclude that
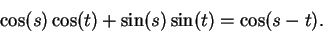 |
(9.16) |
This is equation (9.13). To get equation (9.12) replace  by
by
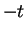 in
(9.16). If we take
in
(9.16). If we take
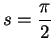 in equation (9.16) we
get
in equation (9.16) we
get
or
If we replace  by
by
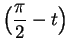 in this equation we get
in this equation we get
Now in equation (9.16) replace 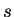 by
by
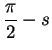 and get
and get
or
which is equation (9.14). Finally replace  by
by 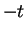 in this last
equation to
get (9.15).
in this last
equation to
get (9.15). 
In the process of proving the last theorem we proved the following:
9.17
Theorem (Reflection law for sin and cos.) For all
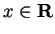 ,
,
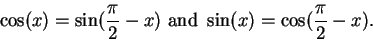 |
(9.18) |
9.19
Theorem (Double angle and half angle formulas.)
For all
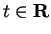 we have
we have
9.20
Exercise.
A
Prove the four formulas stated in theorem
9.19.
Proof: We have
and
By adding these equations, we get (9.22).
By subtracting the first from the
second,
we get (9.24).
In equation (9.24) replace 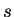 by
by
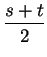 and replace
and replace  by
by
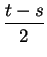 to get
to get
or
This yields equation (9.25).
9.27
Exercise.
Prove equations (
9.23) and (
9.26).
From the geometrical description of sine and cosine, it follows that as  increases
for
increases
for 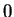 to
to
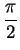 ,
, 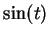 increases from
increases from 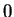 to
to 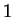 and
and 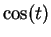 decreases from
decreases from 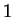 to
to 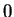 . The identities
. The identities
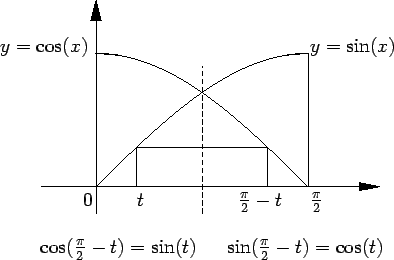
indicate that a reflection about the vertical line through
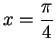 carries
the graph of sin onto the graph of cos, and vice versa.
carries
the graph of sin onto the graph of cos, and vice versa.
The condition
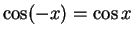 indicates that the reflection
about the
vertical axis carries the graph of
indicates that the reflection
about the
vertical axis carries the graph of 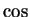 to itself.
to itself.
The relation
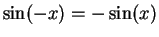 shows that
shows that
i.e., the graph of  is carried onto itself by a rotation through
is carried onto itself by a rotation through  about the origin.
about the origin.
We have
and
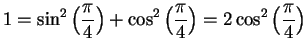 , so
, so
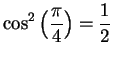 and
and
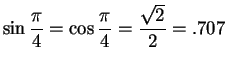 (approximately).
(approximately).
With this information we can make a reasonable sketch of the graph of  and
and  (see the figure above)
(see the figure above)
9.29
Exercise.
A
Complete the following table of sines and cosines:
Include an explanation for how you found
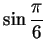 and
and
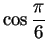 (or
(or
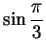 and
and
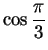 ). For the
remaining values
you do not need to include an explanation.
). For the
remaining values
you do not need to include an explanation.
Most of the material from this section
was discussed by Claudius Ptolemy (fl.
127-151
AD). The functions considered by Ptolemy were not the sine and cosine, but the
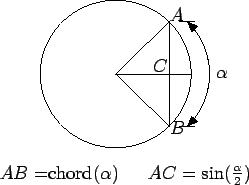
chord, where the chord of an arc 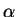 is the length of the segment joining
its
endpoints.
is the length of the segment joining
its
endpoints.
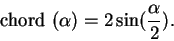 |
(9.30) |
Ptolemy's chords are functions of arcs (measured in degrees), not of numbers.
Ptolemy's
addition law for 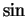 was (roughly)
was (roughly)
where 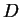 is the diameter of the circle, and
is the diameter of the circle, and
 Ptolemy produced tables equivalent to tables of
Ptolemy produced tables equivalent to tables of 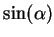 for
for
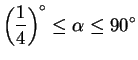 in intervals of
in intervals of
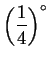 .
All
calculations were made to 3 sexagesimal (base
.
All
calculations were made to 3 sexagesimal (base 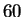 ) places.
) places.
The etymology of the word sine is
rather curious[42, pp 615-616].
The function we call sine was first
given a name by Aryabhata near the start of the sixth century AD.
The name meant ``half chord''
and was later shortened to jya meaning ``chord''. The Hindu
word was translated into Arabic as jîba, which was a meaningless
word phonetically derived from jya, but (because the vowels
in Arabic were not written) was written the same as
jaib, which means bosom. When the Arabic was
translated into Latin it became sinus. (Jaib means bosom, bay,
or breast: sinus means bosom, bay or the fold of a toga around the
breast.) The English word sine is derived from sinus phonetically.
9.31
Entertainment (Calculation of sines.)
Design a computer program that will take as
input a
number

between
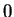
and
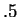
, and will calculate
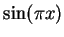
. (I choose
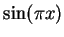
instead of
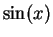
so that you do
not need to know the value of

to do
this.)




Next: 9.2 Calculation of
Up: 9. Trigonometric Functions
Previous: 9. Trigonometric Functions
Index
Ray Mayer
2007-09-07
![]() , then
, then ![]() is the point on the unit circle such that the length
of
the arc joining
is the point on the unit circle such that the length
of
the arc joining ![]() to
to ![]() (measured in the counterclockwise direction)
is
equal to
(measured in the counterclockwise direction)
is
equal to ![]() . (There is an optical illusion
in the figure. The length of segment
. (There is an optical illusion
in the figure. The length of segment ![]() is equal to the length of
arc
is equal to the length of
arc ![]() .)
.)
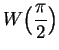
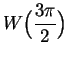
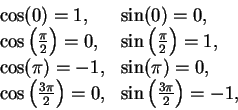
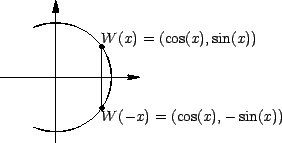
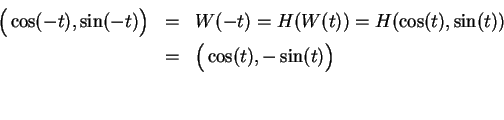
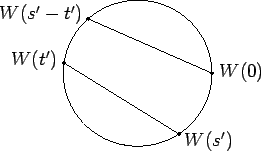
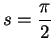 in equation (9.16) we
get
in equation (9.16) we
get
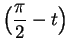 in this equation we get
in this equation we get
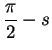 and get
and get
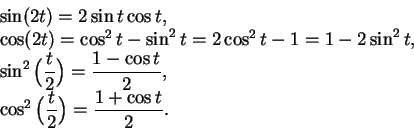
![$\displaystyle {1\over 2}[\cos (s-t)+\cos (s+t)],$](img2377.gif)
![$\displaystyle {1\over 2}[\sin (s+t)-\sin (s-t)],$](img2379.gif)
![$\displaystyle {1\over 2}[\cos (s-t)-\cos (s+t)]
\index{trigonometric identities},$](img2381.gif)
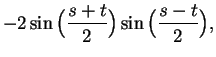
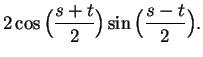
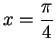 carries
the graph of sin onto the graph of cos, and vice versa.
carries
the graph of sin onto the graph of cos, and vice versa.
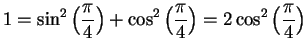 , so
, so
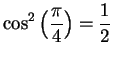 and
and
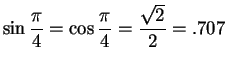 (approximately).
(approximately).
![\begin{displaymath}\begin{array}{\vert l\vert l\vert l\vert l\vert l\vert l\vert...
... &{{\sqrt 2}\over 2} & &0 & & & &-1 [2ex] \hline
\end{array}\end{displaymath}](img2407.gif)
![\begin{displaymath}\begin{array}{\vert l\vert l\vert l\vert l\vert l\vert l\vert...
...hline
\cos &-1 & & & & 0 & & & & 1 [2ex] \hline
\end{array}\end{displaymath}](img2408.gif)
 in intervals of
in intervals of