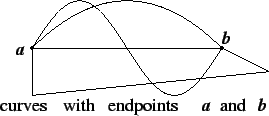
The proof of the next lemma depends on the following assumption, which is explicitly stated by Archimedes [2, page 3]. This assumption involves the ideas of curve with given endpoints and length of curve (which I will leave undiscussed).
Proof:
Case 1: Suppose
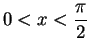 .
.
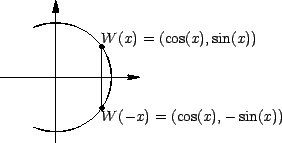
Case 2: Suppose
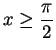 . Then
. Then
Proof: By (9.25) we have
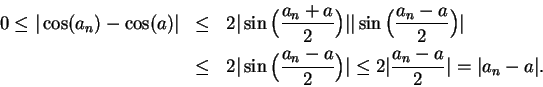
The proof that
![]() is
similar.
is
similar. ![]()
The proof of the next lemma involves another new assumption.
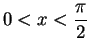 .
Let the tangent to the unit circle at
.
Let the tangent to the unit circle at
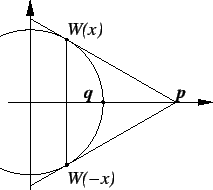
Remark: Archimedes makes a general assumption about curves that are concave in the same direction [2, pages 2-4] which allows him to prove our assumption.
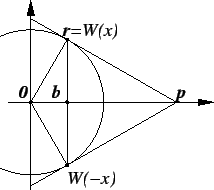
Proof:
Suppose
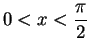 . Draw the tangents to the unit circle at
. Draw the tangents to the unit circle at
![]() and
and
![]() and let the point at which they intersect the
and let the point at which they intersect the ![]() -axis be
-axis be
![]() . (By
symmetry
both tangents intersect the
. (By
symmetry
both tangents intersect the ![]() -axis at the same point.) Let
-axis at the same point.) Let
![]() be the
point where
the segment
be the
point where
the segment ![]() intersects the
intersects the ![]() -axis, and let
-axis, and let
![]() .
Triangles
.
Triangles
![]() and
and
![]() are similar since they are right triangles with a
common acute
angle.
are similar since they are right triangles with a
common acute
angle.
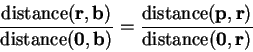

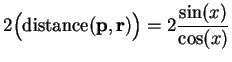 , so by
assumption 9.35,
, so by
assumption 9.35,
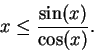
Proof: If
![]() , then it follows from
lemma(9.36) that
, then it follows from
lemma(9.36) that
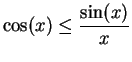 . Since
. Since
Let ![]() be a sequence for which
be a sequence for which ![]() for all
for all
![]() and
and ![]() . Then
we can find a number
. Then
we can find a number
![]() such that for all
such that for all
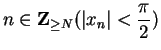 .
By (9.39)
.
By (9.39)
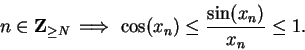
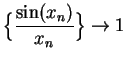 .
.
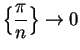 , it follows from
(9.38) that
, it follows from
(9.38) that
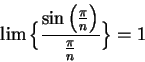
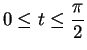 . Here I have used the fact that
. Here I have used the fact that 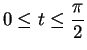 . Also
. Also
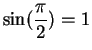 so
so
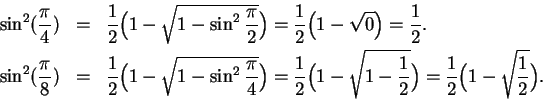
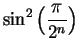 for arbitrary
for arbitrary
I wrote a set of Maple
routines to do
the calculations above. The procedure sinsq(n)
calculates
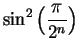 and the procedure
and the procedure
mypi(m)
calculates
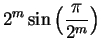 . The `` fi" (which
is
`` if" spelled backwards) is Maple's way of ending an `` if" statement.
`` Digits
. The `` fi" (which
is
`` if" spelled backwards) is Maple's way of ending an `` if" statement.
`` Digits ![]() " indicates that all
calculations are
done to
" indicates that all
calculations are
done to ![]() decimal digits accuracy. The command `` evalf(Pi)" requests
the
decimal approximation to
decimal digits accuracy. The command `` evalf(Pi)" requests
the
decimal approximation to ![]() to be printed.
to be printed.
> sinsq := > n-> if n=1 then 1; > else .5*(1-sqrt(1 - sinsq(n-1))); > fi;sinsq := proc(n) options operator,arrow; if n = 1 then 1 else .5 -.5*sqrt(1-sinsq(n-1)) fi end
> mypi := m -> 2^m*sqrt(sinsq(m));
> Digits := 20;
> mypi(4);
> mypi(8);
> mypi(12);
> mypi(16);
> mypi(20);
> mypi(24);
> mypi(28);
> mypi(32);
> mypi(36);
> mypi(40);
> evalf(Pi);
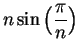 is the area of
a regular
is the area of
a regular