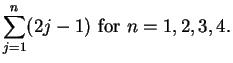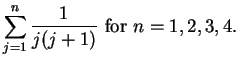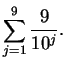Next: 3.5 Mathematical Induction
Up: 3. Propositions and Functions
Previous: 3.3 Functions
Index
Let 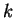 and
and  be integers with
be integers with 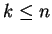 .
Let
.
Let
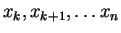 , be real numbers, indexed by the integers
from
, be real numbers, indexed by the integers
from 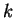 to
to  . We define
. We define
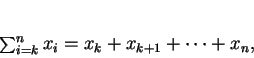 |
(3.53) |
i.e.
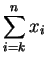 is the sum of all the numbers
is the sum of all the numbers
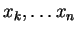 .
A sum of one number is defined to be that number, so that
.
A sum of one number is defined to be that number, so that
The ``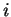 '' in equation (3.53) is a dummy variable, and can be replaced by any symbol that has no meaning assigned to it. Thus
'' in equation (3.53) is a dummy variable, and can be replaced by any symbol that has no meaning assigned to it. Thus
The following properties of the summation notation should be
clear from the definition. (Here
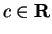 ,
, 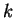 and
and  are integers
with
are integers
with 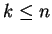 and
and
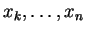 and
and
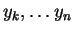 are real
numbers.)
are real
numbers.)
If 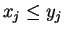 for all
for all 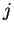 satisfying
satisfying
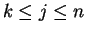 then
then
Also
Using the summation notation, we can rewrite equations (2.9)
and (2.23) as
and
The use of the Greek letter 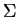 to denote sums was introduced
by Euler in 1755[15, page 61].
Euler writes
to denote sums was introduced
by Euler in 1755[15, page 61].
Euler writes
Compare this with the notation in Bernoulli's table 2.2.
(The apparent difference is due to the fact that for Euler, 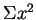 denotes the sum of
denotes the sum of  squares, starting with
squares, starting with 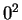 , whereas for
Bernoulli
, whereas for
Bernoulli 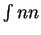 denotes the sum of
denotes the sum of  squares starting with
squares starting with 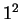 .)
The use of the symbol
.)
The use of the symbol 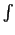 (which is a form of
(which is a form of  ) for sums was
introduced by Leibniz. The
use of limits on sums was introduced by Augustin Cauchy(1789-1857).
Cauchy used the notation
) for sums was
introduced by Leibniz. The
use of limits on sums was introduced by Augustin Cauchy(1789-1857).
Cauchy used the notation
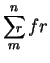 to denote
what we would write
as
to denote
what we would write
as
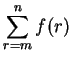 [15, page 61].
[15, page 61].
3.54
Exercise.
Find the following sums:
- a)
-
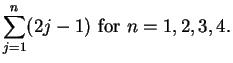
- b)
-
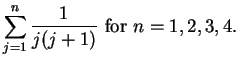
- c)
-
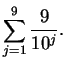




Next: 3.5 Mathematical Induction
Up: 3. Propositions and Functions
Previous: 3.3 Functions
Index
Ray Mayer
2007-09-07
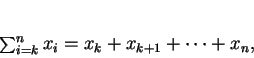
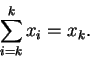
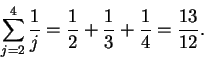
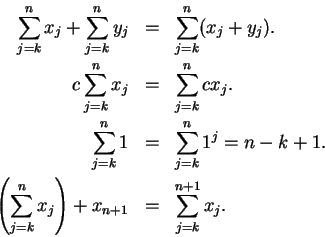
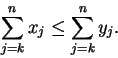
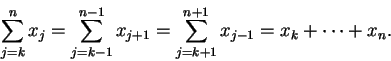
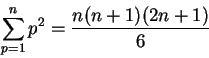
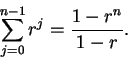
![]() to denote sums was introduced
by Euler in 1755[15, page 61].
Euler writes
to denote sums was introduced
by Euler in 1755[15, page 61].
Euler writes
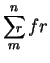 to denote
what we would write
as
to denote
what we would write
as
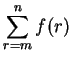 [15, page 61].
[15, page 61].