



Next: 3.4 Summation Notation
Up: 3. Propositions and Functions
Previous: 3.2 Sets Defined by
Index
3.37
Definition (Function.)
Let
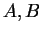
be sets. A
function with domain  and codomain
and codomain 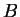
is
an ordered triple
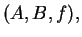
where

is a rule which assigns to each
element of

a unique element of
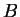
.
The element of
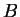
which

assigns to an element

of

is denoted
by
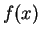
. We call
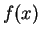
the
 -image of
-image of 
or the
image of  under
under  .
.
The notation
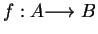
is an abbreviation for ``

is a function
with domain

and codomain
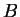
''. We read ``
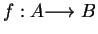
'' as
``

is a function from

to
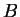
.''
3.38
Examples.
Let
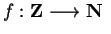
be defined by the rule
Then
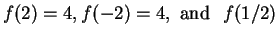
is not defined, because
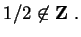
Let
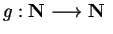 be defined by the rule: for all
be defined by the rule: for all
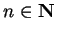
Thus
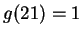
,
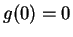
,
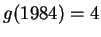
,
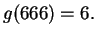
3.39
Definition (Maximum and minimum functions.)
We define functions max and min from

to
R by the rule
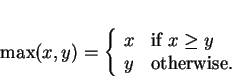 |
(3.40) |
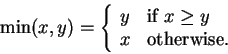 |
(3.41) |
Thus we have
and
for all
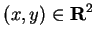 .
Also
.
Also
3.42
Definition (Absolute value function.)
Let
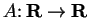
be defined
by the rule
We call

the
absolute value function and we
usually designate
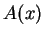
by
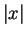
.
3.43
Definition (Sequence)
Let

be a set. A
sequence in

is a function
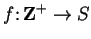
. I will refer to a sequence in
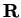
as a
real sequence.
The sequence  is sometimes denoted by
is sometimes denoted by 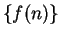 . Thus
. Thus
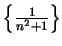 is the sequence
is the sequence
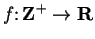 such
that
such
that
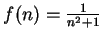 for all
for all
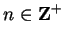 . Sometimes the
sequence
. Sometimes the
sequence  is denoted by
is denoted by
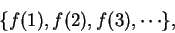 |
(3.44) |
for example
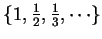 is the same as
is the same as
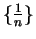 . The notation in formula (3.44) is always
ambiguous. I will use it for sequences like
. The notation in formula (3.44) is always
ambiguous. I will use it for sequences like
in which it is somewhat complicated to give an analytic description for
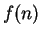 .
.
If  is a sequence, and
is a sequence, and
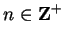 , then we often denote
, then we often denote 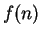 by
by 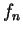 .
.
3.45
Examples.
Let

denote the set of all polygons in the plane. For each number

in
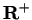
let
For each
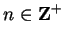
let
and
denote
the polygons inscribed in
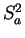
and containing
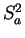
described in section
2.1. Then
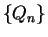 and
and 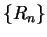 are sequences in
are sequences in  .
.
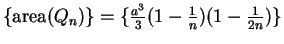 is a real sequence. (Cf. (2.3) and (2.12).)
is a real sequence. (Cf. (2.3) and (2.12).)
![$\{ [ \mbox{area}(Q_n), \mbox{area}(R_n)]\}$](img718.gif) is a sequence of intervals.
is a sequence of intervals.
3.46
Definition (Equality for functions.)
Let
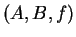
and
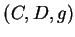
be two functions. Then, since a function is
an ordered triple, we have
The rules

and

are equal
if and only if
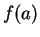
=
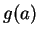
for all
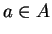
. If
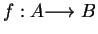
and
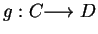
then it is customary to write
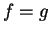
to mean
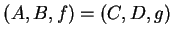
.
This is an abuse of notation, but it is a standard practice.
3.47
Examples.
If
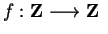
is defined by the rule
and
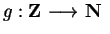
is defined by the rule
then
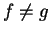
since

and

have different codomains.
If
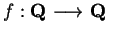 and
and
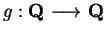 are defined by the
rules
are defined by the
rules
then
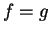
.
In certain applications it is important to know the precise codomain
of a function, but in many applications the precise codomain is not
important, and in such cases I will often omit all mention of the
codomain. For example, I might say ``For each positive number  , let
, let
![$J(a) = [0,a]$](img738.gif) .'' and proceed as though I had defined a function. Here
you could reasonably take the codomain to be
the set of real intervals, or the set of closed intervals, or the set of
all subsets of R.
.'' and proceed as though I had defined a function. Here
you could reasonably take the codomain to be
the set of real intervals, or the set of closed intervals, or the set of
all subsets of R.
3.48
Definition (Image of  )
)
Let
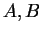
be sets, and let
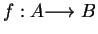
. The set
is called the
image of 
, and is denoted by
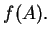
More generally, if
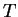
is any subset of

then we define
We call
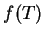
the

-image of
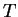
. Clearly, for every
subset
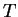
of

we have
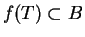
.
3.49
Examples.
If
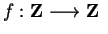
is defined by the rule
then
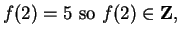
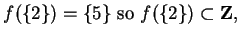
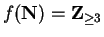 .
.
3.50
Definition (Graph of  )
)
Let
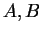
be sets, and let
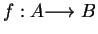
. The
graph of 
is defined
to be
If the domain and codomain of  are subsets of R, then the graph of
are subsets of R, then the graph of
 can be identified with a subset of the plane.
can be identified with a subset of the plane.
3.51
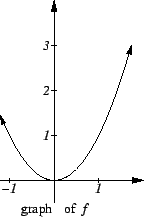
Examples.
Let
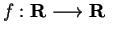
be defined by the rule
The graph of

is sketched below. The arrowheads on the graph are intended
to indicate that the complete graph has not been drawn.
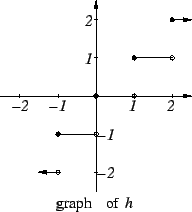
Let
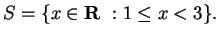 Let
Let  be the function
from
be the function
from  to R defined by the rule
to R defined by the rule
The graph of

is sketched above. The solid dot at
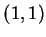
indicates that
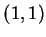
is in the graph. The hollow dot at
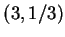
indicates that
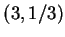
is not in the graph.
Let
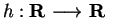 be defined by the rule
be defined by the rule
Thus
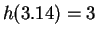
and
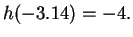
The graph of
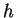
is sketched above.
The term function (functio) was introduced into mathematics
by Leibniz [33, page 272 footnote]. During the
seventeenth century the ideas of function and curve were usually
thought of as being the same, and a curve was often thought of
as the path of a moving point. By the eighteenth century the
idea of function was associated with ``analytic expression''.
Leonard Euler (1707-1783) gave the following definition:
A function of a variable quantity is an analytic expression composed in any way whatsoever of the
variable quantity and numbers or constant quantities.
Hence every analytic expression, in which all component quantities except
the variable 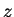 are constants,
will be a
function of that
are constants,
will be a
function of that 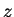 ; Thus
; Thus
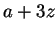 ;
; 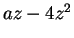 ;
;
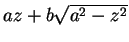 ;
; 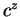 ; etc.
are functions of
; etc.
are functions of 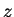 [18, page 3].
[18, page 3].
The use of the notation ``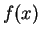 '' to represent the value of
'' to represent the value of  at
at  was introduced by Euler in 1734 [29, page 340].
was introduced by Euler in 1734 [29, page 340].




Next: 3.4 Summation Notation
Up: 3. Propositions and Functions
Previous: 3.2 Sets Defined by
Index
Ray Mayer
2007-09-07
![]() be defined by the rule: for all
be defined by the rule: for all
![]()
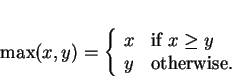
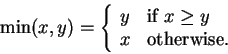
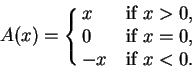
![]() is a sequence, and
is a sequence, and
![]() , then we often denote
, then we often denote ![]() by
by ![]() .
.
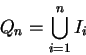
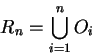
![]() and
and ![]() are sequences in
are sequences in ![]() .
.
![]() is a real sequence. (Cf. (2.3) and (2.12).)
is a real sequence. (Cf. (2.3) and (2.12).)
![]() is a sequence of intervals.
is a sequence of intervals.
![]() and
and
![]() are defined by the
rules
are defined by the
rules
![]() , let
, let
![]() .'' and proceed as though I had defined a function. Here
you could reasonably take the codomain to be
the set of real intervals, or the set of closed intervals, or the set of
all subsets of R.
.'' and proceed as though I had defined a function. Here
you could reasonably take the codomain to be
the set of real intervals, or the set of closed intervals, or the set of
all subsets of R.
![]()
![]() .
.
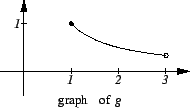
![]() Let
Let ![]() be the function
from
be the function
from ![]() to R defined by the rule
to R defined by the rule
![]() be defined by the rule
be defined by the rule
are constants, will be a function of that
; Thus
;
;
;
; etc. are functions of
[18, page 3].
![]() '' to represent the value of
'' to represent the value of ![]() at
at ![]() was introduced by Euler in 1734 [29, page 340].
was introduced by Euler in 1734 [29, page 340].