



Next: 2.6 Area of a
Up: 2. Some Area Calculations
Previous: 2.4 Finite Geometric Series
Index
The following argument is due to Pierre de Fermat (1601-1665) [19, pages
219-222]. Later we will use Fermat's method to find the area under
the
curve 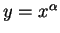 for all
for all 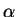 in
in
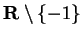 .
.
Let  be a real number with
be a real number with 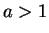 , and let
, and let 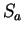 be the set of points
be the set of points 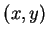 in
in
 such that
such that 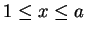 and
and
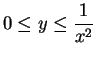 . I
want to
find the area of
. I
want to
find the area of 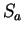 .
.
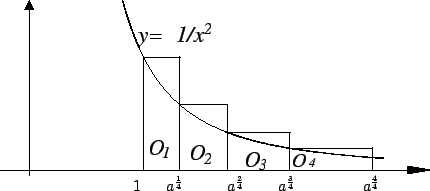
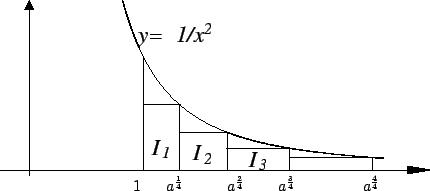
Let  be a positive integer. Note that since
be a positive integer. Note that since 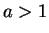 , we have
, we have
Let 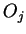 be the box
be the box
Thus the upper left corner of 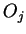 lies on the curve
lies on the curve
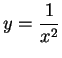 .
.
To simplify the notation, I will write
Then
and
Hence
Observe that we have here a finite geometric series, so
Now
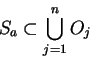 |
(2.32) |
so
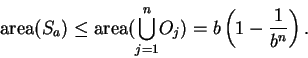 |
(2.33) |
Let 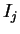 be the box
be the box
so that the upper right corner of 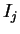 lies on the curve
lies on the curve
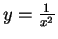 and
and 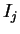 lies
underneath the curve
lies
underneath the curve
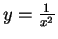 . Then
. Then
Hence,
Since
we have
i.e.,
By combining this result with (2.33), we get
Since
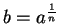 , we can rewrite this as
, we can rewrite this as
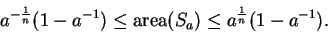 |
(2.34) |
2.35
Exercise.
What do you think the area of
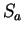
should be? Explain your answer. If
you
have no ideas, take
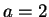
in (
2.34), take large values of

,
and by using a calculator, estimate

to three or
four decimal places of
accuracy.
2.36
Exercise.
A
Let

be a real number with
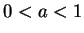
, and let
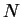
be a positive integer.
Then
Let
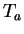
be the set of points
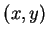
such that
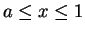
and
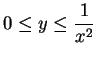
. Draw a sketch of
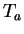
, and show that
The calculation of
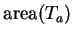
is very similar to the calculation of

.
What do you think the area of 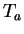 should be?
should be?
2.37
Exercise.
Using the inequalities (
2.6), and the
results of Bernoulli's table in section
2.2, try to guess what
the area of
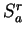
is for an arbitrary positive integer
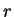
.
Explain the basis for your guess. ( The correct formula for

for positive integers
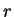
was stated by
Bonaventura Cavalieri in 1647[
6, 122 ff].
Cavalieri also found
a method for computing general positive integer
power sums.)




Next: 2.6 Area of a
Up: 2. Some Area Calculations
Previous: 2.4 Finite Geometric Series
Index
Ray Mayer
2007-09-07
![]() be a real number with
be a real number with ![]() , and let
, and let ![]() be the set of points
be the set of points ![]() in
in
![]() such that
such that ![]() and
and
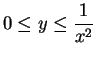 . I
want to
find the area of
. I
want to
find the area of ![]() .
.
![]() be a positive integer. Note that since
be a positive integer. Note that since ![]() , we have
, we have
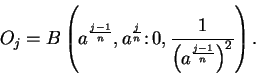
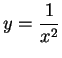 .
.
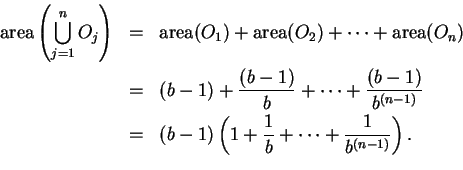
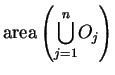
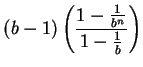
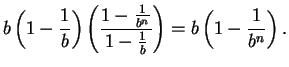
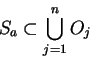
![]() be the box
be the box
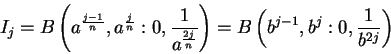
![]() lies on the curve
lies on the curve
![]() and
and ![]() lies
underneath the curve
lies
underneath the curve
![]() . Then
. Then
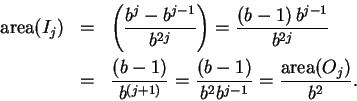
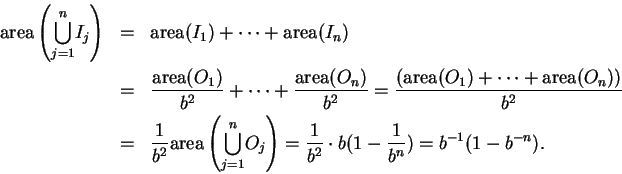
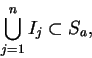
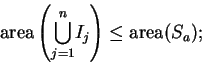
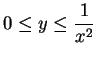 . Draw a sketch of
. Draw a sketch of ![]() should be?
should be?