Math 138: Knot Theory, Knot Practice
Tuesday Thursday 10:30-11:50am, Library 204Office Hours: Tu 3-4, Wed 11-12, Th 3-4, Library 313
Textbook: The Knot Book by Colin Adams
See the poster!
Knot theory, knot practice is an inclusive introduction to modern mathematics through the lens of knot theory. By studying invariants, we will see how the notions of number and algebra come to bear on a fundamental question from topology: when are two knots the same? Topics include
- Reidemeister moves,
- rational tangles,
- Seifert surfaces,
- Vassiliev invariants, and
- applications of knot theory in biology and chemistry.
Week 1
- Tuesday: What is a knot? When are two knots the same?
- Thursday: Read §§1.1-1.3. Projections and Reidemeister moves. Connected sums and prime knots. Assign homework groups.
Homework due Thursday
- Review the syllabus.
- Fill out the office hour doodle. (You were emailed a link.)
- Use one to two pages to answer the following prompts: (1)
Why are you taking this class? (2) What do you hope to learn? (3)
Describe a problem involving knotting which you have encountered in
your life or studies. In what ways might the mathematical study of
knots address this problem?
Like all our assignments, this is a writing assignment. Make sure to use sentences and paragraphs to answer the prompts. (Note that this is an individual assignment, unlike our future group problem sets.)
Week 2
- Tuesday: Read §§1.4-1.5. Links. Tricolorability.
- Thursday: Read §2.3. Tangles.
Homework due Thursday
- 1.2, 1.3 (note special instruction from class), 1.7, 1.8, 1.9, 1.10, 1.11, 1.12.
Week 3
- Tuesday: Read §3.1. Unknotting number.
- Thursday: Read §§3.2-3.3. Bridge and crossing numbers.
- Praxis: Overhand, square, granny, and surgeon's knots.
Homework due Thursday
- 1.16, 1.17, 1.18*, 1.19*, 1.21, 1.25, 1.27, 1.28*
- Using the notation from class, show that the rational tangle A given by applying TTRTRT -1 to the 0 tangle and the rational tangle B given by applying TTRTT to the 0 tangle are equivalent. In fact, do this in two ways: first by finding Reidemeister moves and planar isotopies which take A to B, and then by applying Conway's theorem on the rational numbers associated with A and B.
- Use the algorithm from class to find a sequence of T and R moves which will undo the tangle given by applying TRTTTTTRTTT to the 0 tangle. Is this the shortest sequence of T's and R's which can accomplish the untangling?
- Which (extended) rational numbers can be realized by rational tangles? Prove that your answer is correct.
- Prove that RR takes a rational tangle to an equivalent rational tangle (without invoking Conway's theorem).**
Starred* problems are optional challenge problems. All teams are encouraged to engage with them. Double-starred** problems are optional and extra challenging.
Week 4
- Tuesday: Read §4.1. Surfaces.
- Thursday: Read §4.2. Surfaces with boundary I.
Homework due Thursday
- 3.1, 3.3 (try to come up with the best inequality possible; also prove that your inequality holds for all knots), 3.4, 3.11, 3.13, 3.14, 3.15.
- Adams sketches an argument that two-bridge knots are rational on p.66. Flesh out the argument (or come up with a different one) so that it is more convincing.
- Prove that every 4-plat has bridge number 2 and that every two-bridge knot is a 4-plat.*
Week 5
- Tuesday: Start reading §4.3. Surfaces with boundary II.
- Thursday: Finish reading §4.3. Seifert surfaces.
Homework due Thursday
- 4.10, 4.13, 4.14, 4.15.
- Recall our definition of the Klein bottle K in terms of a square with horizontal sides identified with the same orientation, and vertical sides identified after a half twist. Find a triangulation of K and use it to compute the Euler characteristic of K.
- A model for the ''real projective plane'' P arises from a square by identifying both pairs of opposite sides after half twists. Find a triangulation of P and use it to compute the Euler characteristic of P.
- Suppose that a surface with boundary X arises from a surface without boundary X by removing n disjoint open disks. Determine the genus of X in terms of the Euler characteristic of X.
- Consider the surface O given by identifying sides of a
regular octagon according to the labelling given below. (a) Is this
surface orientable? (b) What is the genus of this surface? (c)
Guided by your answers to (a) and (b), draw a picture of O
after you've glued the edges together. Include the edges in your
picture.
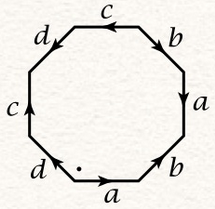
- Construct a model for the orientable genus 3 surface out of a regular polygon with certain sides identified. Prove that your model works by checking that it is orientable and has the correct Euler characteristic.*
- For an arbitrary positive integer n, construct a model for the orientable genus n surface out of a regular polygon with certain sides identified. Prove that your model works by checking that it is orientable and has the correct Euler characteristic.*
Week 6
- Tuesday: Read §5.1. Torus knots.
- Thursday: A practical interlude: knots to know and soap film Seifert surfaces.
No homework this week
Week 7
- Tuesday: Read §6.1. Visualizations of Milnor fibers. The bracket polynomial.
- Thursday: Read §6.2. Applications of knot polynomials to alternating links.
Homework due Thursday
New homework groups were distributed via email.- 5.5, 5.6, 5.7, 5.10
- We described stereographic projection from Sn to n-dimensional Euclidean space in class. Write down an explicit formula for stereographic projection in the n=1 case. Be sure to explain your derivation.
- Write an explicit formula for stereographic projection from S2 to the plane. Be sure to explain your derivation.
- Write an explicit formula for stereographic projection in n=3 case. Either explicitly derive your formula* or explain it via analogy with the n=1,2 cases.
- Derived and write an explicit formula for stereographic projection for an arbitrary n.*
- Show that the intersection of the complex solutions to zp-wq=0 with S3 is a (p,q)-torus knot.**
Enjoy your Fall Break!
Week 8
- Tuesday: Read §6.3. Alexander and HOMFLY polynomials.
- Thursday: Reduced alternating cleanup. Computer packages for knot polynomials. Experiments.
Homework due Thursday
- 6.3, 6.6* (the first sentence of this problem is essentially defining what it means to be a split link), 6.7 (use our computation of the Kauffman polynomial of the [right- or left-handed?] trefoil from class; note that the Jones polynomial is defined directly above this question), 6.8, 6.11, 6.12
- Use a "state tree" to compute the Kauffman polynomial of the figure eight knot.
- Prove that for any oriented link L, X(L*) is equal to X(L) but with all of the a's replaced with a-1's, i.e., X(L*)(a) = X(L)(a-1). (Here L* refers to the mirror image of L.) Use this result to describe the form X(L) must take when L is amphichiral, i.e., L=L*. (Despite the *'s, this is not a bonus problem!)
- Prove that for any oriented links L, M, X(L#M) = X(L)·X(M). (There is some ambiguity here since there are choices about where to connect the links. Nonetheless, the formula holds for any of these choices.)*
Week 9
- Tuesday: HOMFLY polynomials; more fun with polynomial invariants.
- Thursday: Read §5.4. Braids.
Homework due Thursday
- Complete the exercises in this pdf.
Week 10
- Tuesday: Markov moves, Markov traces.
- Thursday: The Temperley-Lieb algebra. Distribute second midterm (due Tuesday, November 17).
Homework due Thursday
- 5.16, 5.17, 5.19, 5.20, 5.21, 5.22, 5.28, 5.29, 6.20(a), 6.20(b)*
Week 11
- Tuesday: The Temperley-Lieb algebra, continued. [PDF of Kauffman on Markov traces and the Temperley-Lieb algebra]
- Thursday: Read Adams §7.1. DNA topology.
No homework this week.
Week 12
- Tuesday: Links in graphs.
- Thursday: No class. Happy Thanksgiving!
Homework due Thursday
- Compute the Kauffman polynomial of (an orientation of) the Whitehead link 512 via the Temperley-Lieb algebra.
- The (2,n)-torus link is the closure of the braid σ1n. Use the Temperley-Lieb algebra to find a closed form expression for the Kauffman and Jones polynomials of this link. (You will need to use the binomial theorem in order to expand a certain expression.)
- Use Exercise 5.22 and the Temperley-Lieb algebra to find a closed form for the Kauffman polynomial of the (m,n)-torus knot, m,n relatively prime.*
- Solve the puzzle posed in class about single loop TL compositions 0 → 2n → 0. (A good answer should consist of a method for enumerating all sequences of "caps and cups" which compose to give single loop diagrams. An even better answer will answer the similar question where "single" is replaced with k for any k between 1 and n.)*
- Explain what it means for ρ and the bracket on the Temperley-Lieb algebra to "respect" the first and second Markov moves.
- Prove that the specific properties you stated in the previous problem do in fact hold.*
Week 13
- Tuesday: Knotted Hamiltonian cycles. Conway-Gordon [pdf].
- Thursday: What is a knot (redux)? Reidemeister moves. Course evaluations.
Homework due Tuesday, December 8.
- 8.2, 8.3*, 8.4, 8.6, 8.7, 8.11, 8.12, 8.13, 8.15
Week 14
- Tuesday: Guest lecture by Steve Bleiler. Final homework due. Distribrute take-home final.
The LaTeX document preparation system
Poor handwriting? Love escape characters? Too much free time? Try LaTeX!
- LaTeX at Reed.
- A short guide [pdf] to writing mathematics with LaTeX.
- To add graphics, you'll want the \includegraphics command and a good source of knot diagrams. There are a number of good suggestions here.
Kyle M. Ormsby