



Next: Bibliography
Up: 17. Antidifferentiation Techniques
Previous: 17.6 Substitution in Integrals
Index
17.7 Rational Functions
In this section we present a few rules for finding antiderivatives of simple
rational
functions.
To antidifferentiate
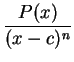 where
where  is a polynomial,
make
the substitution
is a polynomial,
make
the substitution 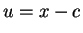 .
.
17.56
Example.
To find
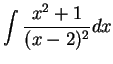
.
Let 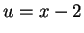 . Then
. Then 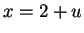 so
so 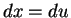 , and
, and
To find
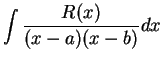 where
where 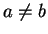 and
and 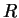 is a
polynomial of degree less than
is a
polynomial of degree less than 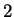 .
.
We will find numbers  and
and 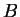 such that
such that
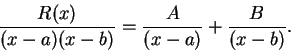 |
(17.57) |
Suppose (17.57) were valid. If we multiply both sides by 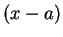 we
get
we
get
Now take the limit as  goes to
goes to  to get
to get
The reason I took a limit here, instead of saying ``now for 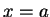 we get
we get
 '' is that
'' is that  is not in the domain of the function we are
considering.
Similarly
is not in the domain of the function we are
considering.
Similarly
and if we take the limit as  goes to
goes to  , we get
, we get
Thus,
![\begin{displaymath}
{{R(x)}\over {(x-a)(x-b)}}={1\over {a-b}}\Bigg[ {{R(a)}\over
{x-a}}-{{R(b)}\over {x-b}}\Bigg].
\end{displaymath}](img4341.gif) |
(17.58) |
I have now shown that if there are numbers  and
and 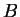 such that
(17.57) holds, then (17.58) holds. Since I have
not shown that such numbers exist, I will verify directly that
(17.58) is valid.
Write
such that
(17.57) holds, then (17.58) holds. Since I have
not shown that such numbers exist, I will verify directly that
(17.58) is valid.
Write 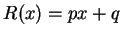 . Then
. Then
17.59
Example.
To find
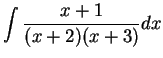
.
Let
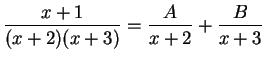 .
.
Then
so
and
so
Hence
In this example I did not use formula (
17.58), because I find it
easier to remember the procedure than the general formula. I do not
need to check my answer, because my proof of (
17.58) shows that
the procedure always works. (In practice, I usually do check the result
because I am likely to make an arithmetic error.)
To find
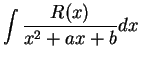 where
where 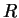 is a polynomial of
degree
is a polynomial of
degree
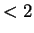 , and
, and 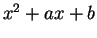 does not factor as a product of two first degree
polynomials.
does not factor as a product of two first degree
polynomials.
Complete the square to write
Then 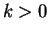 , since if
, since if 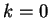 then we have factored
then we have factored 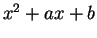 , and if
, and if 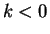 we
can write
we
can write 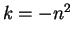 , and then
, and then
and again we get a factorization of 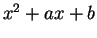 . Since
. Since 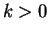 , we can write
, we can write
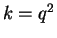 for
some
for
some
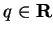 , and
, and
Now
Make the substitution 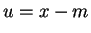 to get an antiderivative of the form
to get an antiderivative of the form
The last antiderivative can be found by a trigonometric substitution.
17.60
Example.
To find
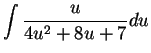
:
Let
Let
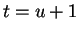
, so
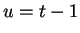
and
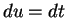
. Then
Now let
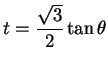
, so
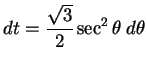
, and
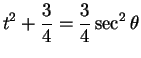
.
Then
Hence,
To find
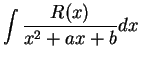 where
where 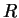 is a polynomial of
degree
is a polynomial of
degree
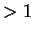 .
.
First use long division to write
where 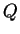 is a polynomial, and
is a polynomial, and  is a polynomial of degree
is a polynomial of degree 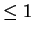 . Then
use one
of the methods already discussed.
. Then
use one
of the methods already discussed.
17.61
Example.
To find
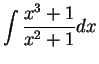
.
By using long division, we get
Hence
17.62
Example.
In exercise
17.7, you showed that
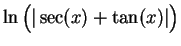
is an antiderivative for
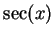
. The function
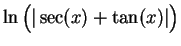
in that exercise appeared magically with no
motivation. I will now derive the formula, using standard methods:
Now let
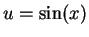
. Then
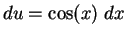
, and
Suppose

. Then
and if we take the limit of both sides as
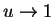
we get
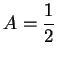
.
Also
and if we take the limit as
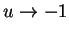
, we get
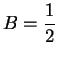
. Thus
Now
so
and thus
17.63
Exercise.
Criticize the following argument:
I want to find
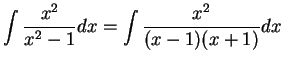 . Suppose
. Suppose
Then
If we take the limit of both sides as
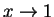
, we get
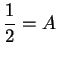
.
Also
and if we take the limit of both sides as
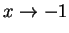
, we get
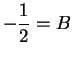
.
Thus
Hence,
17.64
Exercise.
Find the following antiderivatives:
- a)
-
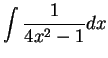
- b)
-
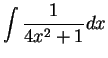
- c)
-
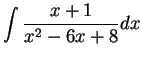
- d)
-
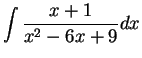
- e)
-
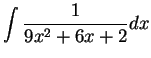
- f)
-
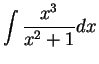
- g)
-
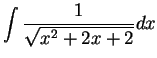 A
A




Next: Bibliography
Up: 17. Antidifferentiation Techniques
Previous: 17.6 Substitution in Integrals
Index
Ray Mayer
2007-09-07
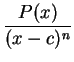 where
where 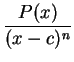 where
where ![]() is a polynomial,
make
the substitution
is a polynomial,
make
the substitution ![]() .
.
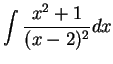 .
.
![]() . Then
. Then ![]() so
so ![]() , and
, and
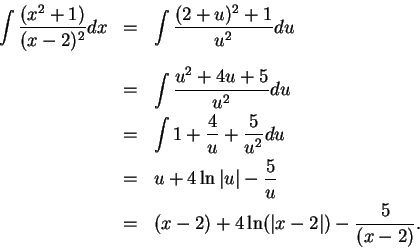
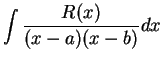 where
where ![]() and
and ![]() is a
polynomial of degree less than
is a
polynomial of degree less than ![]() .
.
![]() and
and ![]() such that
such that
![]() we
get
we
get 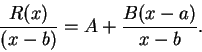
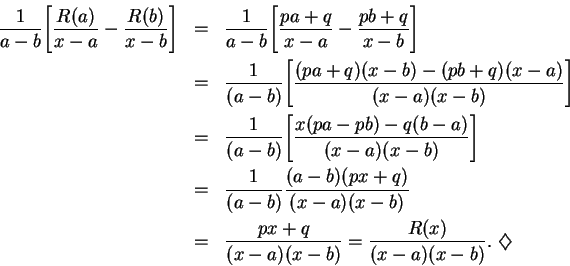
 .
.
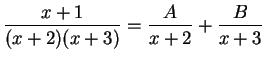 .
.
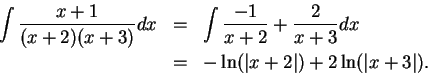
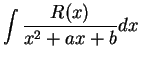 where
where ![]() is a polynomial of
degree
is a polynomial of
degree
![]() , and
, and ![]() does not factor as a product of two first degree
polynomials.
does not factor as a product of two first degree
polynomials.
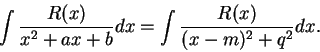
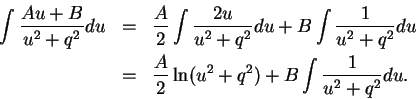
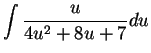 :
:
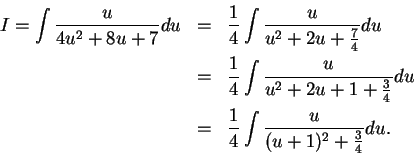
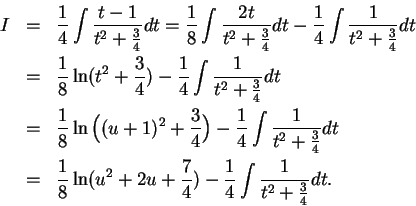
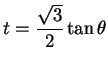 , so
, so
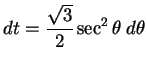 , and
, and
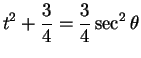 .
Then
.
Then
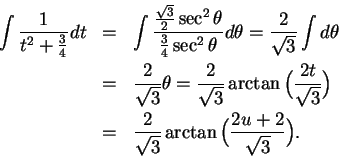
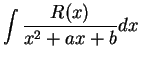 where
where ![]() is a polynomial of
degree
is a polynomial of
degree
![]() .
.
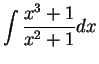 .
By using long division, we get
.
By using long division, we get
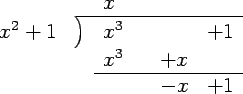
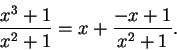
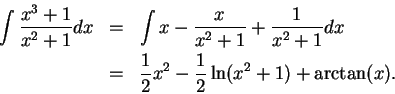
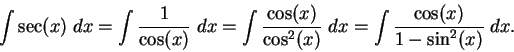
 . Then
. Then
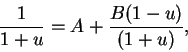
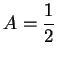 .
Also
.
Also
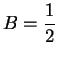 . Thus
. Thus
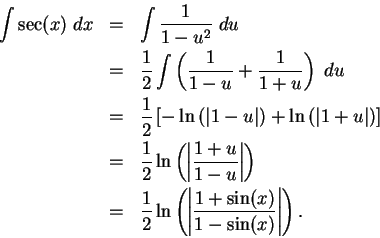
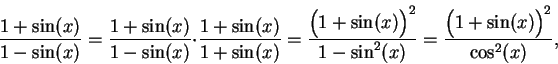
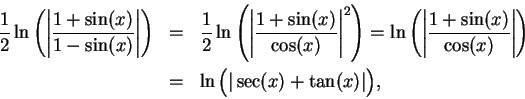
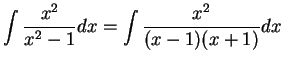 . Suppose
. Suppose
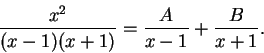
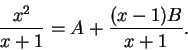
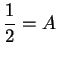 .
Also
.
Also
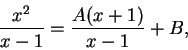
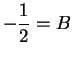 .
Thus
.
Thus
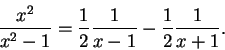
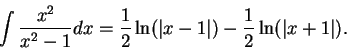
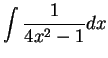
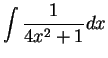
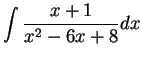
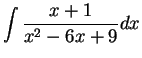
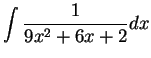
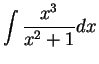
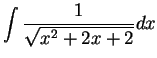 A
A
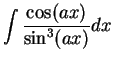 .
.
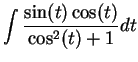 .
.
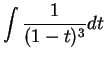 .
.
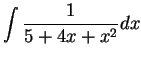 .
.
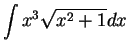 .
.
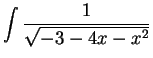 .
.
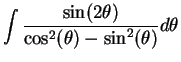 .
.
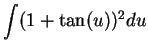 .
.
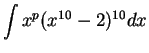 .
.
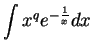 .
.
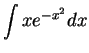 .
.
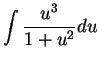 .
.
 .
.
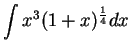 .
.
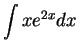 .
.
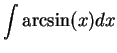 .
.