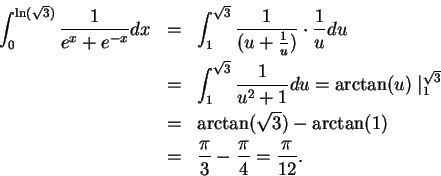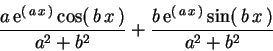Next: 17.7 Rational Functions
Up: 17. Antidifferentiation Techniques
Previous: 17.5 Trigonometric Substitution
Index
17.6 Substitution in Integrals
Let  be a nice function on an interval
be a nice function on an interval ![$[a,b]$](img1071.gif) . Then if
. Then if 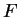 is any
antiderivative
for
is any
antiderivative
for  , we have
, we have
by the fundamental theorem of calculus. We saw in (17.32) that under
suitable hypotheses on  ,
, 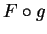 is an antiderivative for
is an antiderivative for 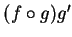 .
Hence
.
Hence
Hence we can find
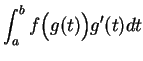 by the following
ritual:
by the following
ritual:
Let 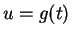 . When
. When 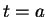 then
then 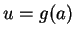 and when
and when 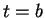 then
then 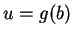 . Also
. Also
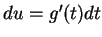 . Hence
. Hence
17.51
Example.
To find
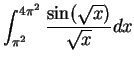
.
Let 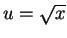 . When
. When 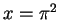 , then
, then 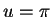 , and when
, and when 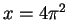 , then
, then 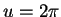 .
Also
.
Also
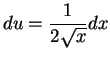 , so
, so
We saw in (17.36) that if  is an inverse function for
is an inverse function for  , then an
antiderivative for
, then an
antiderivative for 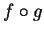 is
is 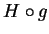 , where
, where 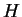 is an antiderivative for
is an antiderivative for
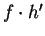 . Thus
. Thus
The ritual
for finding
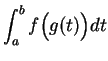 in this case is:
in this case is:
Let 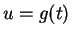 . Then
. Then 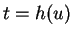 and
and 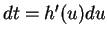 . When
. When 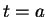 then
then 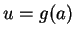 , and
when
, and
when
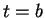 then
then 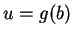 . Thus
. Thus
where 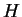 is an antiderivative for
is an antiderivative for 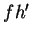 .
.
17.52
Example.
To find
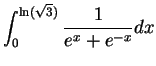
.
Let 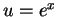 . When
. When 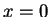 then
then 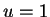 , and when
, and when
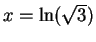 then
then 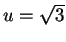 .
Also
.
Also
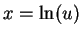 , so
, so
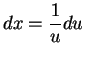 .
.
17.53
Exercise.
A
Find the following integrals:
- a)
-
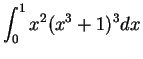 .
.
- b)
-
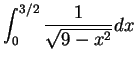 .
.
- c)
-
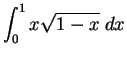 .
.
17.54
Exercise.
A
Find the area of the shaded region, bounded by the ellipse
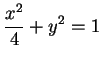
and the lines
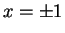
.
17.55
Example.
In practice I would find many of the antiderivatives and integrals
discussed
in this chapter by computer. For example, using Maple, I would find
> int(sqrt(a^2+x^2),x);
> int(sin(sqrt(x)),x=0..Pi^2);
> int(sqrt(4 - x^2),x=-1..1);
> int( (sec(x))^3,x);
> int(exp(a*x)*cos(b*x),x);




Next: 17.7 Rational Functions
Up: 17. Antidifferentiation Techniques
Previous: 17.5 Trigonometric Substitution
Index
Ray Mayer
2007-09-07
![]() be a nice function on an interval
be a nice function on an interval ![]() . Then if
. Then if ![]() is any
antiderivative
for
is any
antiderivative
for ![]() , we have
, we have
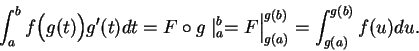
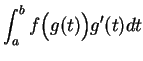 by the following
ritual:
by the following
ritual:
![]() . When
. When ![]() then
then ![]() and when
and when ![]() then
then ![]() . Also
. Also
![]() . Hence
. Hence
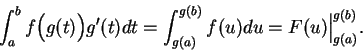
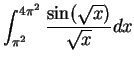 .
.
![]() . When
. When ![]() , then
, then ![]() , and when
, and when ![]() , then
, then ![]() .
Also
.
Also
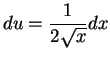 , so
, so
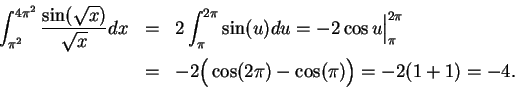
![]() is an inverse function for
is an inverse function for ![]() , then an
antiderivative for
, then an
antiderivative for ![]() is
is ![]() , where
, where ![]() is an antiderivative for
is an antiderivative for
![]() . Thus
. Thus
 in this case is:
in this case is:
![]() . Then
. Then ![]() and
and ![]() . When
. When ![]() then
then ![]() , and
when
, and
when
![]() then
then ![]() . Thus
. Thus
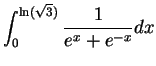 .
.
![]() . When
. When ![]() then
then ![]() , and when
, and when
![]() then
then ![]() .
Also
.
Also
![]() , so
, so
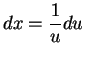 .
.