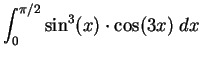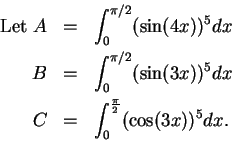Next: 10. Definition of the
Up: 9. Trigonometric Functions
Previous: 9.3 Integrals of the
Index
9.57
Theorem.
Let 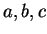 be real numbers. If
be real numbers. If  is a function that is integrable on each
interval
with endpoints in
is a function that is integrable on each
interval
with endpoints in 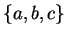 then
then
Proof: The case where
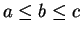 is proved in
theorem 8.18. The rest of
the proof is
exactly like the proof of exercise 5.69.
is proved in
theorem 8.18. The rest of
the proof is
exactly like the proof of exercise 5.69. 
9.58
Exercise.
Prove theorem
9.57.
We have proved the following formulas:
In each case we have a formula of the form
This is a general sort of situation, as is shown by the following theorem.
Proof: Choose a point 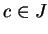 and define
and define
Then for any points 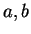 in
in  we have
we have
We've used the fact that
9.62
Definition (Indefinite integral.)
Let

be a function that is integrable on
every subinterval
of an interval

. An
indefinite integral for  on
on 
is any
function
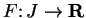
such that
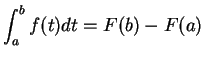
for all
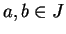
.
A function that has an indefinite integral always has infinitely many
indefinite integrals,
since if 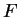 is an indefinite integral for
is an indefinite integral for  then so is
then so is 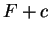 for any number
for any number 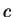 :
:
The following notation is used for indefinite integrals. One writes 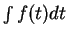 to denote
an indefinite integral for
to denote
an indefinite integral for  . The
. The  here is a dummy variable and can be
replaced by any
available symbol. Thus, based on formulas (9.59) - (9.60),
we
write
here is a dummy variable and can be
replaced by any
available symbol. Thus, based on formulas (9.59) - (9.60),
we
write
We might also write
Some books always include an arbitrary constant with indefinite integrals,
e.g.,
The notation for indefinite integrals is treacherous. If you see the
two equations
and
then you want to conclude
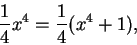 |
(9.63) |
which is wrong.
It would be more logical to let the symbol 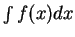 denote the set
of all indefinite integrals for
denote the set
of all indefinite integrals for  . If you see the statements
. If you see the statements
and
you are not tempted to make the conclusion in (9.63).
Proof:
The statement (9.65) means that if 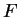 is an indefinite integral
for
is an indefinite integral
for  and
and 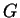 is an indefinite integral for
is an indefinite integral for 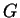 , then
, then
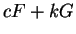 is an indefinite integral for
is an indefinite integral for 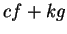 .
.
Let 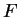 be an indefinite integral for
be an indefinite integral for  and let
and let 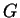 be an indefinite integral
for
be an indefinite integral
for  .
Then for all
.
Then for all 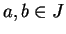
It follows that 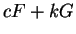 is an indefinite integral for
is an indefinite integral for 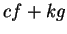 .
. 
9.66
Notation (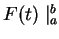 .)
.)
If
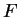
is a function defined on an interval

,
and if
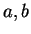
are
points in

we write
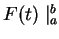
for
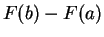
. The

here is a dummy
variable,
and sometimes the notation is ambiguous, e.g.
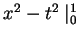
. In such cases
we may write
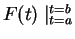
. Thus
while
Sometimes we write
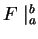
instead of
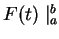
.
9.67
Example.
It follows from our notation that if
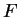
is an indefinite integral for

on an
interval

then
and this notation is used as follows:
In the last example I have implicitly used
9.68
Example.
By using the trigonometric identities from theorem
9.21 we can
calculate
integrals of the form
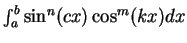
where
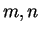
are
non-negative integers
and
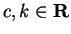
. We will find
We have
so
Thus
Hence
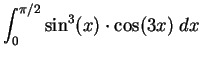
The method here is clear, but a lot of writing is involved, and there are many
opportunities
to make errors. In practice I wouldn't do a calculation of this sort by hand.
The Maple
command
> int((sin(x))^3*cos(3*x),x=0..Pi/2);
responds with the value
- 5/12
9.69
Exercise.
A
Calculate the integrals
Then determine the values of
without doing any calculations. (But include an explanation of where your
answer comes
from.)
9.71
Exercise.
Arrange the numbers
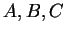
in increasing order. Try to do the problem without
making any
explicit calculations. By making rough sketches of the graphs you should be
able to come up
with the answers. Sketch the graphs, and explain how you arrived at your
conclusion. No
`` proof" is needed.




Next: 10. Definition of the
Up: 9. Trigonometric Functions
Previous: 9.3 Integrals of the
Index
Ray Mayer
2007-09-07
![]() and define
and define
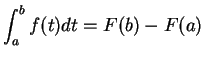 for all
for all ![]() is an indefinite integral for
is an indefinite integral for ![]() then so is
then so is ![]() for any number
for any number ![]() :
:
![]() to denote
an indefinite integral for
to denote
an indefinite integral for ![]() . The
. The ![]() here is a dummy variable and can be
replaced by any
available symbol. Thus, based on formulas (9.59) - (9.60),
we
write
here is a dummy variable and can be
replaced by any
available symbol. Thus, based on formulas (9.59) - (9.60),
we
write
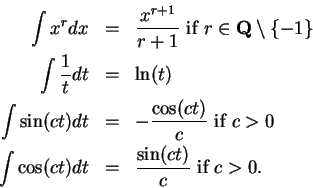
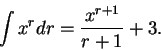
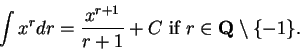
![]() is an indefinite integral
for
is an indefinite integral
for ![]() and
and ![]() is an indefinite integral for
is an indefinite integral for ![]() , then
, then
![]() is an indefinite integral for
is an indefinite integral for ![]() .
.
![]() be an indefinite integral for
be an indefinite integral for ![]() and let
and let ![]() be an indefinite integral
for
be an indefinite integral
for ![]() .
Then for all
.
Then for all ![]()
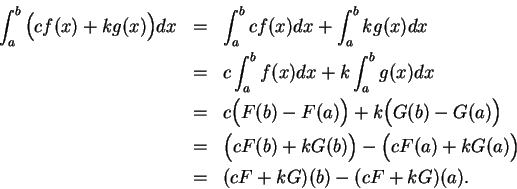
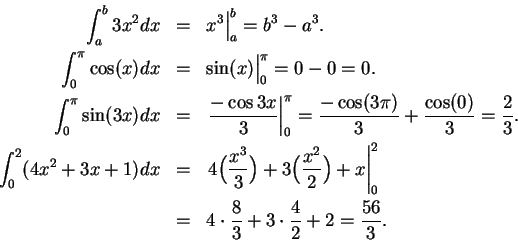
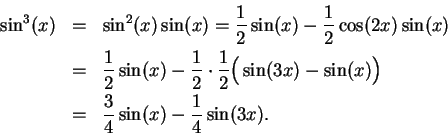
![\begin{eqnarray*}
\sin^3 (x)\cdot\cos (3x) &=& {3\over 4}\cos (3x)\sin (x)-{1\ov...
...3x)\\
&=& {3\over 8}[\sin (4x)-\sin (2x) ]-{1\over 8}\sin (6x).
\end{eqnarray*}](img2609.gif)