



Next: 7. Still More Area
Up: 6. Limits of Sequences
Previous: 6.6 Geometric Series
Index
6.81
Example.
We will calculate
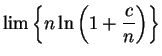
, where
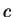
is a positive number.
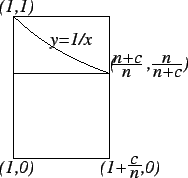
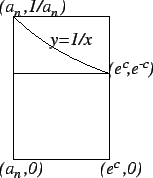
Let
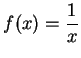
. Then (see the figure)
and hence
Thus
i.e.
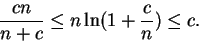 |
(6.82) |
Since
it follows from the squeezing rule that
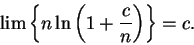 |
(6.83) |
Notice that in this example the squeezing rule has allowed us to
prove the existence of a limit whose existence was not obvious.
6.84
Example.
We will show that for all
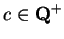
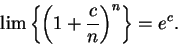 |
(6.85) |
Let
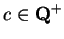
, and let
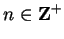
.
Let
By (
6.82), we have
so
It follows from (
6.83) that
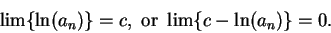 |
(6.86) |
From the picture, we see that
i.e.
Hence
By (
6.86), we have
so by the squeezing rule,
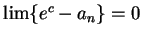
, i.e.
This completes the proof of (
6.85).
The reason we assumed 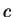 to be positive in the previous example
was to guarantee that
to be positive in the previous example
was to guarantee that
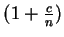 has a logarithm.
We could extend this proof to work for arbitrary
has a logarithm.
We could extend this proof to work for arbitrary
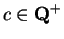 ,
but we suggest an alternate proof for negative
,
but we suggest an alternate proof for negative 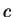 in exercise 6.97
in exercise 6.97
6.87
Example (Numerical calculation of 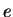 )
)
It follows from the last example that
I wrote a Maple
procedure to calculate
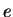
by using this
fact. The procedure
limcalc(n) below calculates
and I have printed out the results for n = 1,2,...,6.
> limcalc := n -> (1+ .01^n)^(100^n);
> limcalc(1);
> limcalc(2);
> limcalc(3);
> limcalc(4);
> limcalc(5);
> limcalc(6);
6.88
Exercise.
From my computer calculations it appears that
Explain what has gone wrong. What can I conclude about the value of
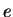
from my program?
6.89
Example.
Actually, Maple is smart enough to find the limit, and does so with
the commands below. The command
evalf returns the decimal
approximation of its argument.
> limit( (1+1/n)^n,n=infinity);
> evalf(%);
6.90
Entertainment (
 .)
.)
Find the
limit of the sequence
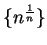
, or else show that
the sequence diverges.
6.91
Example (Compound interest.)
The previous exercise has the following interpretation.
Suppose that  dollars is invested at
dollars is invested at 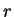 % annual interest,
compounded
% annual interest,
compounded  times a year. The value of the investment at any time
times a year. The value of the investment at any time
 is calculated as follows:
is calculated as follows:
Let
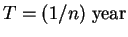 , and let
, and let 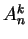 be the value of the investment at
time
be the value of the investment at
time 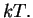 Then
Then
and in general
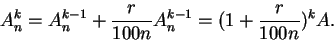 |
(6.93) |
The value of the investment does not change during the time interval
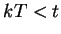
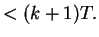
For example, if
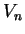
denotes the value of one dollar invested
for one year at
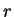
% annual rate of
interest with the interest compounded

times a
year, then
Thus it follows from our calculation that if one dollar is invested
for one year at 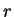 % annual rate of interest, with the interest compounded
``infinitely often'' or ``continuously'', then the value of the investment
at the end of the year will be
% annual rate of interest, with the interest compounded
``infinitely often'' or ``continuously'', then the value of the investment
at the end of the year will be
If the rate of interest is 100%, then the value of the investment
is
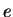
dollars, and the investor should expect
to get $2.71 from the bank.
This example was considered by Jacob Bernoulli in 1685. Bernoulli was able to show that
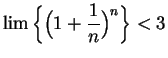 .[8, pp94-97]
.[8, pp94-97]
6.94
Exercise.
Calculate the following limits.
- A
- a)
-
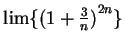 .
.
- b)
-
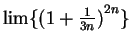 .
.
6.95
Exercise.
- a)
- Use the formula for a finite geometric series,
to show that
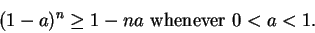 |
(6.96) |
- b)
- Let
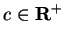 Use inequality (6.96) to show that
Use inequality (6.96) to show that
for all
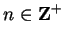 such that
such that 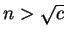 .
.
- c)
- Prove that
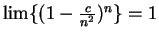 for all
for all
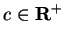 .
.
6.97
Exercise.
A
Let
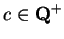
.
Use exercise
6.95 to show that
(Hence we have
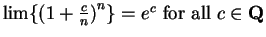
.)
Hint: Note that
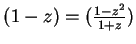 for all real numbers
for all real numbers 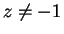 .
.




Next: 7. Still More Area
Up: 6. Limits of Sequences
Previous: 6.6 Geometric Series
Index
Ray Mayer
2007-09-07
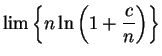 , where
, where
 . Then (see the figure)
. Then (see the figure)
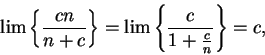
![]() to be positive in the previous example
was to guarantee that
to be positive in the previous example
was to guarantee that
![]() has a logarithm.
We could extend this proof to work for arbitrary
has a logarithm.
We could extend this proof to work for arbitrary
![]() ,
but we suggest an alternate proof for negative
,
but we suggest an alternate proof for negative ![]() in exercise 6.97
in exercise 6.97
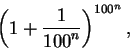
![]() dollars is invested at
dollars is invested at ![]() % annual interest,
compounded
% annual interest,
compounded ![]() times a year. The value of the investment at any time
times a year. The value of the investment at any time
![]() is calculated as follows:
is calculated as follows:
![]() , and let
, and let ![]() be the value of the investment at
time
be the value of the investment at
time ![]() Then
Then
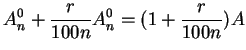
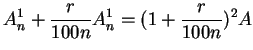
![]() % annual rate of interest, with the interest compounded
``infinitely often'' or ``continuously'', then the value of the investment
at the end of the year will be
% annual rate of interest, with the interest compounded
``infinitely often'' or ``continuously'', then the value of the investment
at the end of the year will be
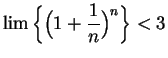 .[8, pp94-97]
.[8, pp94-97]
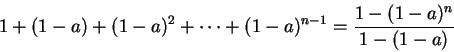
![]() for all real numbers
for all real numbers ![]() .
.