Equation (6.74) is often written in the form
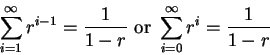
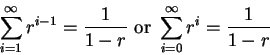
Proof: Let ![]() be a real number such that
be a real number such that ![]() , and
for all
, and
for all
![]() let
let
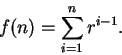
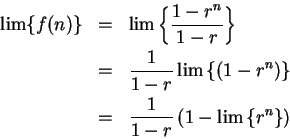
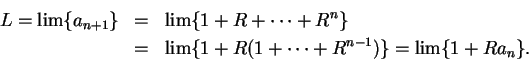
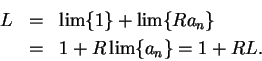
``The clearest early account of the summation of geometric series''[6, page 136] was given by Grégoire de Saint-Vincent in 1647. Grégoire's argument is roughly as follows:
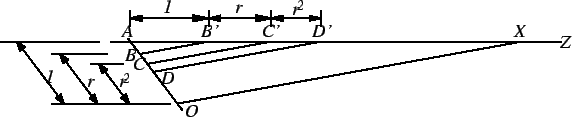
On the line ![]() mark off points
mark off points ![]() ,
, ![]() ,
, ![]() etc. such that
etc. such that
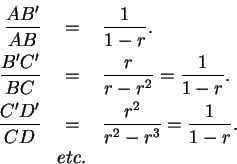
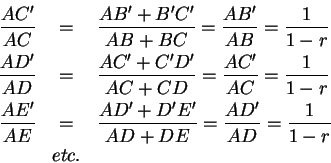
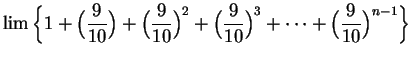 .
.
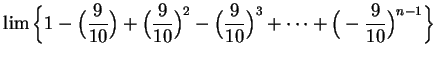 .
.
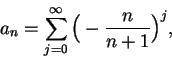
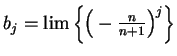 depends on
depends on