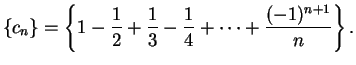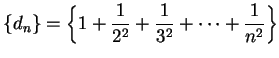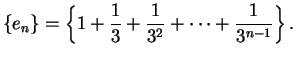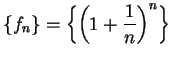Next: 6.4 Properties of Limits.
Up: 6. Limits of Sequences
Previous: 6.2 Approximation
Index
6.19
Definition (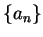 converges to
converges to 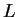 .)
.)
Let 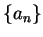 be a sequence of real numbers, and let
be a sequence of real numbers, and let 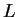 be a real number. We
say
that
be a real number. We
say
that 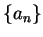 converges to
converges to 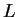 if for every positive number
if for every positive number 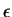 there
is a number
there
is a number 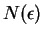 in
in
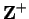 such that all of the numbers
such that all of the numbers 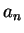 for
which
for
which
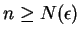 approximate
approximate 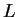 with an error smaller than
with an error smaller than 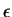 . We
denote the fact that
. We
denote the fact that 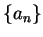 converges to
converges to 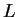 by the notation
by the notation
Thus ``
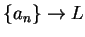
" means:
For every
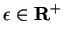 there is a number
there is a number 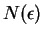 in
in
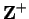 such that
such that
Since
it follows immediately from the definition of convergence that
We will make frequent use of these equivalences.
6.20
Example.
If
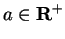
then
Proof: Let 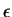 be a generic element of
be a generic element of
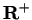 . I must find a number
. I must find a number
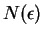 such that
such that
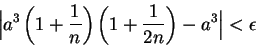 |
(6.21) |
whenever
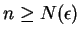
. Well, for all

in
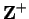
Now for every

in
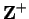
we have
and by the Archimedean property of
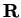
there is some integer
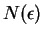
such
that
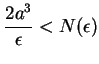
. For all
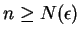
we
have
so by (
6.22)
Hence by the definition of convergence we have
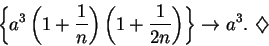 |
(6.23) |
A very similar argument can be used to show that
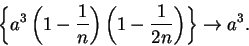 |
(6.24) |
6.25
Example.
In the eighteenth century the rather complicated argument just
given would have been stated as
If  is infinitely large, then
is infinitely large, then
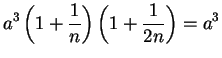 .
.
The first calculus text book (written by Guillaume François
de l'Hôpital
and published in 1696) sets forth the postulate
Grant that two quantities, whose difference is an infinitely
small quantity, may be taken (or used) indifferently for each other:
or (which is the same thing) that a quantity which is increased or decreased
only by an infinitely small quantity, may be considered as remaining
the same[35, page 314].
If

is infinite, then
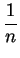
is infinitely small, so
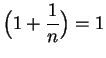
, and similarly
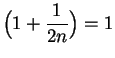
.
Hence
There were numerous objections to this sort of reasoning. Even though
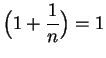
, we do not have
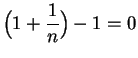
, since
It took many mathematicians working over hundreds
of years to come up with our definition of convergence.
6.26
Theorem (Uniqueness theorem for convergence.)
Let 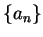 be a sequence of real numbers, and let
be a sequence of real numbers, and let 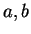 be real
numbers. Suppose
Then
be real
numbers. Suppose
Then 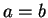 .
.
Proof: Suppose 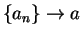 and
and 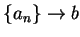 . By the triangle
inequality
. By the triangle
inequality
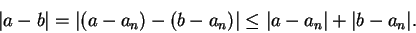 |
(6.27) |
Let 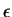 be a generic element of
be a generic element of
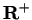 . Then
. Then
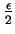 is also in
is also in
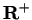 . Since
. Since 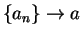 , there is a number
, there is a number
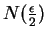 in
in
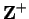 such that
such that
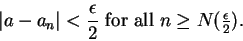 |
(6.28) |
Since 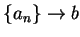 there is a number
there is a number
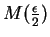 in
in
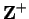 such that
such that
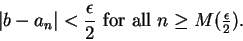 |
(6.29) |
Let 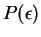 be the larger of
be the larger of
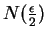 and
and
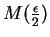 . If
. If  is a positive integer
and
is a positive integer
and
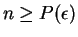 then by (6.27), (6.28), and
(6.29), we have
then by (6.27), (6.28), and
(6.29), we have
Since this holds for all 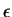 in
in
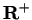 , we have
, we have 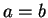 .
. 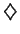
6.30
Definition (Limit of a sequence.)
Let
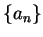
be a sequence of real numbers. If there is a number

such that
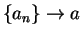
, we write
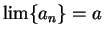
. The uniqueness
theorem for convergence shows that this definition makes sense. If
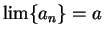
, we say
 is the limit of the sequence
is the limit of the sequence 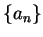 .
.
6.31
Definition (Convergent and divergent sequence.)
Let
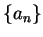
be a sequence of real numbers. If there is a number

such that
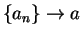
, we say that
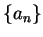
is a
convergent
sequence. If there is no such number

, we say that
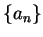
is a
divergent sequence.
6.32
Example.
It follows from example
6.20 that
for all

in
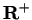
. Hence
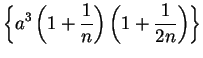
is a convergent sequence
for each

in
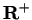
.
The sequence 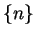 is a divergent sequence. To see this, suppose there
were a number
is a divergent sequence. To see this, suppose there
were a number  such that
such that 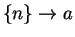 .
.
Then we can find a number
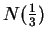 such that
such that
In particular
(since
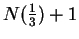
is an integer
greater than
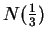
).
Hence, by the triangle inequality
i.e.,
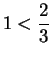
which is false.
Since the assumption 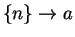 has led to a contradiction, it is false
that
has led to a contradiction, it is false
that 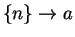 .
. 
6.33
Exercise.
A
Let
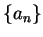
be a sequence of real numbers,
and let

be a real number. Suppose that as

gets larger and larger,
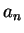
gets nearer and nearer to

, i.e., suppose that for all
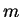
and

in
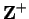
Does it follow that
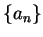
converges to

?




Next: 6.4 Properties of Limits.
Up: 6. Limits of Sequences
Previous: 6.2 Approximation
Index
Ray Mayer
2007-09-07
![]() be a sequence of real numbers, and let
be a sequence of real numbers, and let ![]() be a real number. We
say
that
be a real number. We
say
that ![]() converges to
converges to ![]() if for every positive number
if for every positive number ![]() there
is a number
there
is a number ![]() in
in
![]() such that all of the numbers
such that all of the numbers ![]() for
which
for
which
![]() approximate
approximate ![]() with an error smaller than
with an error smaller than ![]() . We
denote the fact that
. We
denote the fact that ![]() converges to
converges to ![]() by the notation
by the notation
![]() there is a number
there is a number ![]() in
in
![]() such that
such that
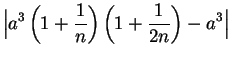
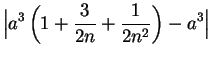
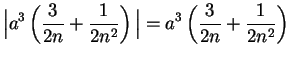
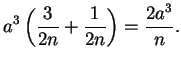
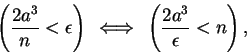
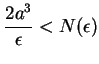 . For all
. For all
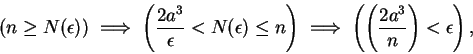
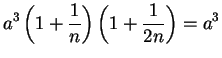 .
.
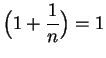 , and similarly
, and similarly
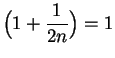 .
Hence
.
Hence
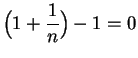 , since
, since
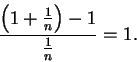
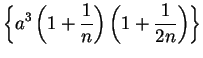 is a convergent sequence
for each
is a convergent sequence
for each 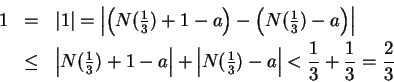
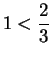 which is false.
which is false.