



Next: 6.3 Convergence of Sequences
Up: 6. Limits of Sequences
Previous: 6.1 Absolute Value
Index
6.12
Definition ( approximates
approximates  .)
.)
Let
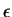
be a positive number, and let

and

be arbitrary numbers.
I will say that
 approximates
approximates  with an error smaller than
with an error smaller than 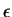
if
and only if
Remark: If  approximates
approximates  with an error smaller than
with an error smaller than
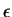 , then
, then  approximates
approximates  with an error smaller than
with an error smaller than 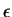 ,
since
,
since
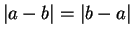 .
.
6.13
Definition (Approximation to  decimals.)
decimals.)
Let
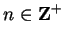
, and let
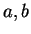
be real numbers. I will say that
 approximates
approximates  with
with  decimal accuracy
decimal accuracy if and only if

approximates

with an error smaller than
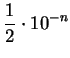
; i.e., if and only
if
6.14
Notation.
If I write three dots (
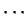
) at the end of a number written in
decimal notation, I assume that all of the digits before the three
dots are correct. Thus since
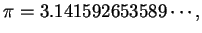
I have
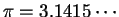
, and
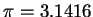
with 4 decimal accuracy.
6.15
Example.
and
Hence
and
Hence
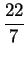
approximates

with an error smaller than
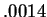
,
and
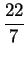
approximates

with 2 decimal accuracy.
6.16
Example.
We see that
and
but there is no two digit decimal that approximates
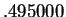
with 2 decimal
accuracy.
6.17
Example.
Since
we see that
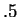
approximates
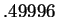
with 4 decimal accuracy, even though
the two numbers have no decimal digits in common.
Since
we see that
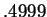
does not approximate
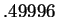
with 4 decimal
accuracy, even though the two numbers have four decimal digits in common.
6.18
Theorem (Strong approximation theorem.) Let  and
and  be real numbers. Suppose that for every positive number
be real numbers. Suppose that for every positive number
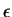 ,
,  approximates
approximates  with an error smaller than
with an error smaller than 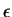 . Then
. Then
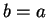 .
.
Proof: Suppose that  approximates
approximates  with an error smaller than
with an error smaller than
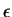 for every positive number
for every positive number 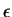 . Then
. Then
Hence
i.e.,
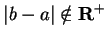 . But
. But
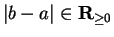 , so it follows that
, so it follows that
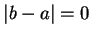 , and consequently
, and consequently 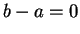 ; i.e.,
; i.e., 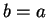 .
. 




Next: 6.3 Convergence of Sequences
Up: 6. Limits of Sequences
Previous: 6.1 Absolute Value
Index
Ray Mayer
2007-09-07
![]() approximates
approximates ![]() with an error smaller than
with an error smaller than
![]() , then
, then ![]() approximates
approximates ![]() with an error smaller than
with an error smaller than ![]() ,
since
,
since
![]() .
.
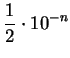 ; i.e., if and only
if
; i.e., if and only
if
![]() approximates
approximates ![]() with an error smaller than
with an error smaller than
![]() for every positive number
for every positive number ![]() . Then
. Then