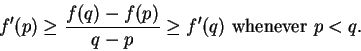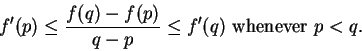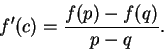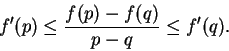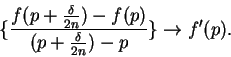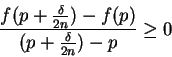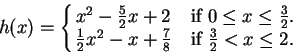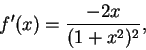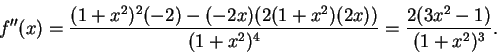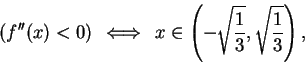Next: 16. Fundamental Theorem of
Up: 15. The Second Derivative
Previous: 15.2 Acceleration
Index
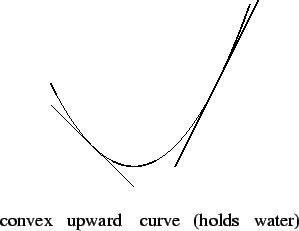
15.24
Definition (Convexity)
Let

be a differentiable function on an interval

. We say that

is
convex upward over 
or that
 holds water over
holds water over 
if and only if for each point

in

, the tangent line to graph(

) at
lies below the graph of

.
Since the equation of the tangent line to graph(

) at
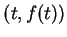
is
the condition for

to be convex upward over

is that for all

and

in

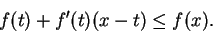 |
(15.25) |
Condition (
15.25) is equivalent to the two conditions:
and
These last two conditions can be written as the single condition
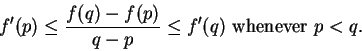 |
(15.26) |
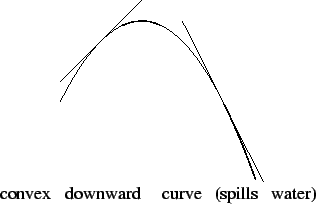
We say that  is convex downward over
is convex downward over  , or that
, or that  spills
water over
spills
water over  if and only if for each point
if and only if for each point  in
in  ,
the tangent line to graph(
,
the tangent line to graph( ) at
) at
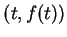 lies above the graph of
lies above the graph of  .
.
This condition is equivalent to the condition that for all points
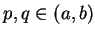
15.27
Theorem.
Let  be a differentiable function over the interval
be a differentiable function over the interval  .
Then
.
Then  is convex upward over
is convex upward over  if and only if
if and only if 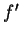 is increasing
over
is increasing
over  . (and similarly
. (and similarly  is convex downward over
is convex downward over  if and only
if
if and only
if 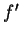 is decreasing over
is decreasing over  .)
.)
Proof: If  is convex upward over
is convex upward over  , then it follows from
(15.26) that
, then it follows from
(15.26) that 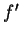 is increasing over
is increasing over  .
.
Now suppose that 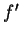 is increasing over
is increasing over  . Let
. Let 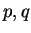 be distinct points
in
be distinct points
in  . By the mean value theorem there is a point
. By the mean value theorem there is a point 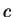 between
between 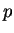 and
and
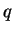 such that
such that
If 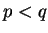 then
then 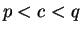 so since
so since 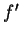 is increasing over
is increasing over 
i.e.
Thus condition (15.26) is satisfied, and  is convex upward over
is convex upward over
 .
.
15.28
Corollary.
Let  be a function such that
be a function such that 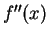 exists for
all
exists for
all  in the interval
in the interval  . If
. If 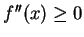 for all
for all 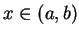 then
then  is convex upward over
is convex upward over  . If
. If 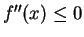 for all
for all
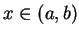 then
then  is convex downward over
is convex downward over  .
.
15.29
Exercise.
A
Prove one of the two statements in
corollary
15.28.
15.30
Lemma (Converse of corollary 12.26) Let  be a real
function such that
be a real
function such that  is continuous on
is continuous on ![$[a,b]$](img1071.gif) and differentiable on
and differentiable on
 . If
. If  is increasing on
is increasing on ![$[a,b]$](img1071.gif) , then
, then 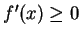 for all
for all
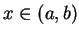 .
.
Proof: let 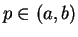 . Choose
. Choose 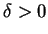 such that
such that
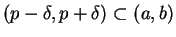 . Then
. Then
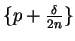 is a sequence such that
is a sequence such that
and hence
Since  is increasing on
is increasing on  , we have
, we have
for all
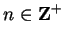 , and it follows that
, and it follows that
15.31
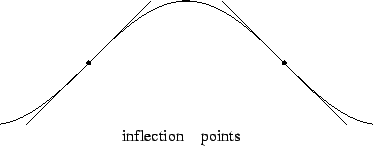
Definition (Inflection point)
Let

be a real function,
and let
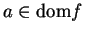
. We say that

is a
point of inflection
for

if there is some
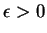
such that
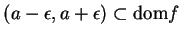
, and

is convex upward on one of the intervals
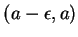
,
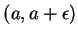
, and
is convex downward on the other.
15.32
Theorem (Second derivative test for inflection points) Let  be a real function, and let
be a real function, and let  be a point of inflection for
be a point of inflection for  . If
. If 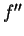 is defined and continuous in some
interval
is defined and continuous in some
interval
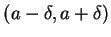 then
then
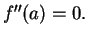
Proof: We will suppose that  is convex upward on the interval
is convex upward on the interval
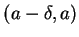 and is convex downward on
and is convex downward on 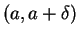 . (The proof in the
case where these conditions are reversed is essentially the same).
Then
. (The proof in the
case where these conditions are reversed is essentially the same).
Then 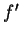 is increasing on
is increasing on 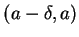 , and
, and 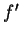 is decreasing on
is decreasing on 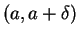 . By (15.30),
. By (15.30), 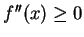 for all
for all
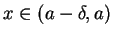 , and
, and 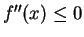 for all
for all
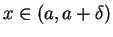 .
We have
.
We have
and
It follows that 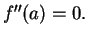
15.33
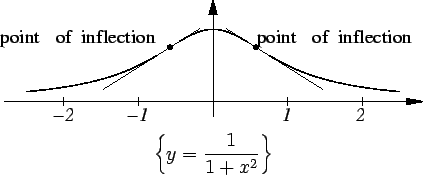
Example.
When you look at the graph of a function, you can usually ``see'' the
points where the second derivative changes sign. However, most people
cannot ``see'' points where the second derivative is undefined.
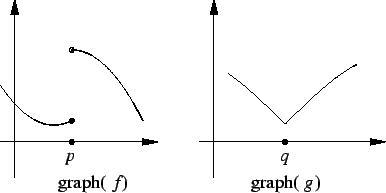
By inspecting graph
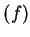
, you can see that

has a discontinuity at
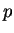
.
By inspecting graph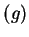 , you can see that
, you can see that  is continuous everywhere,
but
is continuous everywhere,
but 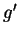 is not defined at
is not defined at 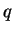 .
.
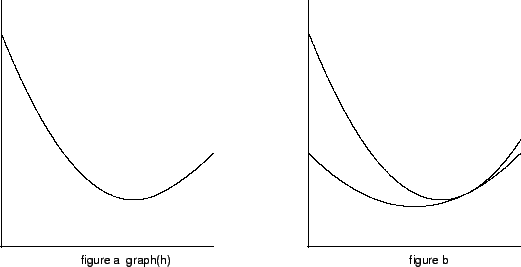
By inspecting graph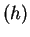 in figure a below, you can see
that
in figure a below, you can see
that 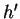 is continuous, but
you may have a hard time seeing the point where
is continuous, but
you may have a hard time seeing the point where 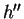 is not defined.
is not defined.
The function 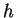 is defined by
is defined by
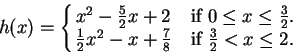 |
(15.34) |
so
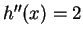
for
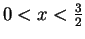
, and
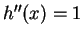
for
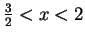
, and
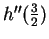
is not defined. We constructed
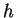
by
pasting together two parabolas. Figure b shows the two
parabolas, one having a second derivative equal to 1, and the other having
second derivative equal to 2.
15.35
Exercise.
Let
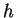
be the function described
in formula (
15.34). Draw graphs of
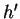
and
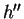
.
15.36
Entertainment (Discontinuous derivative problem.)
There exists a function

such that

is differentiable
everywhere on
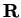
, but
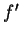
is discontinuous somewhere. Find such a function.
15.37
Exercise.
Let
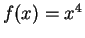
. Show that
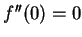
, but
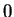
is not
a point of inflection for

. Explain why this result does not contradict
theorem
15.32
15.38
Example.
Let
Then
and
Thus the only critical point for

is
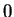
. Also,
so

is increasing on
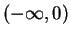
and is decreasing on
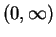
.
Thus

has a maximum at
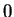
, and

has no minima.
We see that
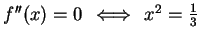 , and moreover
, and moreover
so

spills water over the interval
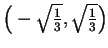
,
and

holds water over each of the intervals
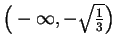
and
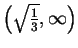
.
Thus

has points of inflection at
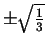
.
We can use all of this information to make a
reasonable sketch of the graph of

.
Note that
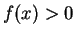
for all

,
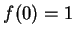
, and
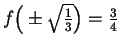
, and
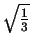
is approximately 0.58.
15.39
Exercise.
Discuss the graphs of the following functions. Make
use of all the information that you can get by looking at the functions
and their first two derivatives.
a)
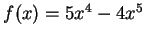 .
.
b)
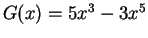 .
.
c)
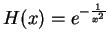 .
.




Next: 16. Fundamental Theorem of
Up: 15. The Second Derivative
Previous: 15.2 Acceleration
Index
Ray Mayer
2007-09-07
![]() is convex downward over
is convex downward over ![]() , or that
, or that ![]() spills
water over
spills
water over ![]() if and only if for each point
if and only if for each point ![]() in
in ![]() ,
the tangent line to graph(
,
the tangent line to graph(![]() ) at
) at
![]() lies above the graph of
lies above the graph of ![]() .
.