Next: 13. Applications
Up: 12. Extreme Values of
Previous: 12.3 Maxima and Minima
Index
12.24
Lemma (Rolle's Theorem)
Let 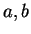 be real numbers with
be real numbers with 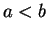 and let
and let
![$f\colon
[a,b]\to\mbox{{\bf R}}$](img2208.gif) be a
function that is continuous on
be a
function that is continuous on ![$[a,b]$](img1071.gif) and differentiable on
and differentiable on  . Suppose
that
. Suppose
that
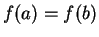 . Then there is a point
. Then there is a point 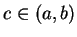 such that
such that
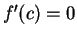 .
.
Proof: By the extreme value property,  has a maximum at some point
has a maximum at some point ![$A\in
[a,b]$](img3209.gif) . If
. If 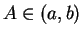 , then
, then
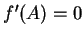 by the critical point theorem.
Suppose
by the critical point theorem.
Suppose 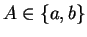 . By the extreme value property,
. By the extreme value property,  has a minimum at
some point
has a minimum at
some point ![$B\in [a,b]$](img3213.gif) . If
. If 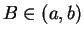 then
then
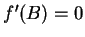 by the critical
point
theorem. If
by the critical
point
theorem. If 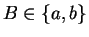 , then we have
, then we have
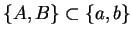 so
so
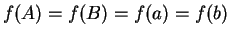 . Hence in this case the maximum value and the minimum value taken by
. Hence in this case the maximum value and the minimum value taken by
 are equal, so
are equal, so 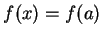 for
for ![$x\in [a,b]$](img1976.gif) so
so
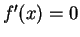 for all
for all 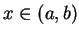 .
. 
Rolle's theorem is named after Michel Rolle (1652-1719). An English
translation of
Rolle's original statement and proof of the theorem can be found in [43, pages
253-260]. It takes a considerable effort to see any relation between
what
Rolle says and what our form of Rolle's theorem says.
12.25
Theorem (Mean value theorem.)
Let 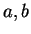 be real numbers and let
be real numbers and let
![$f\colon
[a,b]\to\mbox{{\bf R}}$](img2208.gif) be a function that is
continuous on
be a function that is
continuous on ![$[a,b]$](img1071.gif) and differentiable on
and differentiable on  . Then there is a point
. Then there is a point
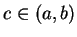 such that
such that
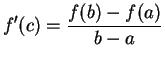 ; i.e.,
there
is a point
; i.e.,
there
is a point
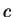 where the slope of the tangent line is equal to the slope of the line
joining
where the slope of the tangent line is equal to the slope of the line
joining
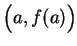 to
to
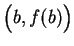 .
.
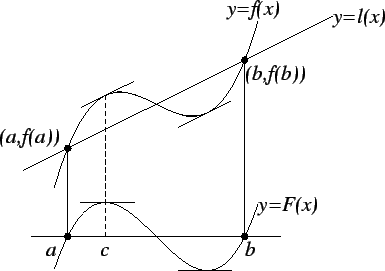
Proof: The equation of the line joining
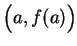 to
to
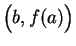 is
is
Let
Then 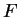 is continuous on
is continuous on ![$[a,b]$](img1071.gif) and differentiable on
and differentiable on  and
and
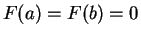 .
By Rolle's theorem there is a point
.
By Rolle's theorem there is a point 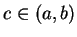 where
where
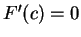 .
.
Now
so
12.26
Corollary.
Let  be an interval in
be an interval in
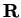 and let
and let
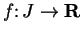 be a function that is
continuous on
be a function that is
continuous on  and differentiable at the interior points of
and differentiable at the interior points of  . Then
. Then
Proof: I will prove the second assertion. Suppose
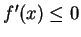 for all
for all
 . Let
. Let 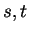 be points in
be points in  with
with 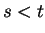 . Then by the mean value
theorem
. Then by the mean value
theorem
Since
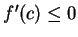 and
and 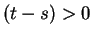 , we have
, we have
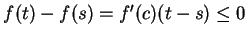 ; i.e.,
; i.e., 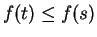 . Thus
. Thus  is decreasing on
is decreasing on
12.27
Exercise.
A
Prove the first assertion of the previous corollary; i.e., prove that if

is continuous on an interval

, and
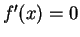
for all

,
then

is constant on

.
12.28
Definition (Antiderivative)
Let

be a real valued function with
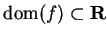
. Let

be an
interval such that
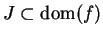
. A function
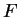
is an
antiderivative for 
on

if
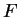
is continuous on

and
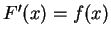
for all

in
the interior of

.
12.29
Examples.
Since
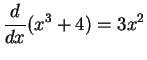
, we see that
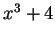
is an
antiderivative for
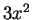
.
Since
and
we see that
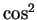
and
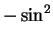
are
both antiderivatives for
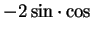
.
We will consider the problem of finding antiderivatives in chapter
17. Now I just want to make the following observation:
12.31
Exercise.
A
Prove the antiderivative theorem.
12.32
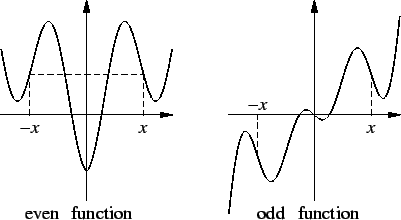
Definition (Even and odd functions.)
A subset

of
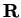
is called
symmetric if
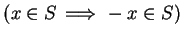
. A
function

is said to be
even if
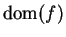
is a symmetric subset of
and
and

is said to be
odd if
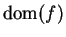
is a symmetric subset of
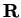
and
.
12.33
Example.
If
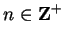
and
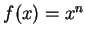
, then

is even if

is even, and

is odd if

is odd. Also
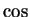
is an even function and
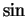
is an odd
function,
while
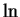
is neither even or odd.
12.34
Example.
If

is even, then
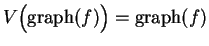
where
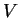
is
the reflection about the vertical axis. If

is odd, then
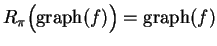
where
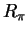
is a rotation by

about the
origin.
12.35
Exercise.
A
Are there any functions that are both
even and odd?
12.36
Exercise.
A
- a)
- If
 is an arbitrary even differentiable
function, show that the derivative of
is an arbitrary even differentiable
function, show that the derivative of  is odd.
is odd.
- b)
- If
 is an arbitrary odd differentiable
function, show that the derivative of
is an arbitrary odd differentiable
function, show that the derivative of  is even.
is even.




Next: 13. Applications
Up: 12. Extreme Values of
Previous: 12.3 Maxima and Minima
Index
Ray Mayer
2007-09-07
![]() has a maximum at some point
has a maximum at some point ![]() . If
. If ![]() , then
, then
![]() by the critical point theorem.
Suppose
by the critical point theorem.
Suppose ![]() . By the extreme value property,
. By the extreme value property, ![]() has a minimum at
some point
has a minimum at
some point ![]() . If
. If ![]() then
then
![]() by the critical
point
theorem. If
by the critical
point
theorem. If ![]() , then we have
, then we have
![]() so
so
![]() . Hence in this case the maximum value and the minimum value taken by
. Hence in this case the maximum value and the minimum value taken by
![]() are equal, so
are equal, so ![]() for
for ![]() so
so
![]() for all
for all ![]() .
. ![]()
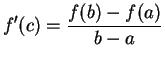 ; i.e.,
there
is a point
; i.e.,
there
is a point
![]() to
to
![]() is
is
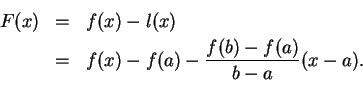
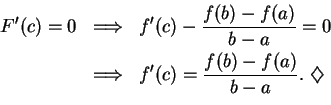
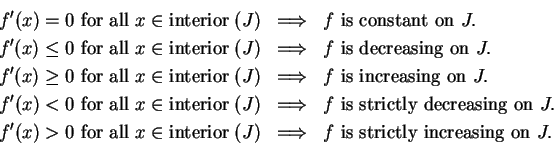
![]() for all
for all
![]() . Let
. Let ![]() be points in
be points in ![]() with
with ![]() . Then by the mean value
theorem
. Then by the mean value
theorem
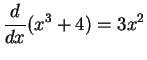 , we see that
, we see that