



Next: 17. Antidifferentiation Techniques
Up: Math 111 Calculus I
Previous: 15.3 Convexity
Index
16.1
Definition (Nice functions.)
I will say that a real valued function

defined on an interval
![$[a,b]$](img1071.gif)
is a
nice function on
![$[a,b]$](img1071.gif)
, if

is continuous on
![$[a,b]$](img1071.gif)
and integrable on every subinterval of
![$[a,b]$](img1071.gif)
.
Remark: We know that piecewise monotonic continuous functions on ![$[a,b]$](img1071.gif) are
nice. It turns out that every continuous function on
are
nice. It turns out that every continuous function on ![$[a,b]$](img1071.gif) is nice, but we
are not
going to prove this. The theorems stated in this chapter for nice functions
are usually stated for continuous functions. You can find a proof that every
continuous
function on an interval
is nice, but we
are not
going to prove this. The theorems stated in this chapter for nice functions
are usually stated for continuous functions. You can find a proof that every
continuous
function on an interval ![$[a,b]$](img1071.gif) is integrable on
is integrable on ![$[a,b]$](img1071.gif) (and hence that every
continuous function on
(and hence that every
continuous function on ![$[a,b]$](img1071.gif) is nice on
is nice on ![$[a,b]$](img1071.gif) ) in [44, page 246]
or in
[1, page 153]. However both of these sources use a slightly
different
definition of continuity and of integral than we do, so you will need to do
some work
to translate the proofs in these references into proofs in our terms. You
might try
to prove the result yourself, but the proof is rather tricky. For all the
applications we will make in this course, the functions examined will be
continuous
and piecewise monotonic so the theorems as we prove them are good enough.
) in [44, page 246]
or in
[1, page 153]. However both of these sources use a slightly
different
definition of continuity and of integral than we do, so you will need to do
some work
to translate the proofs in these references into proofs in our terms. You
might try
to prove the result yourself, but the proof is rather tricky. For all the
applications we will make in this course, the functions examined will be
continuous
and piecewise monotonic so the theorems as we prove them are good enough.
16.2
Exercise.
A
Can you give an example of a continuous function on a closed interval
that is
not piecewise monotonic?
You may describe your example rather loosely, and you do not need to
prove that it is continuous.
Proof: By the definition of antiderivative, 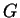 is continuous on
is continuous on ![$[a,b]$](img1071.gif) and
and
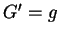 on
on  . Let
. Let 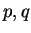 be arbitrary points in
be arbitrary points in ![$[a,b]$](img1071.gif) . I will
suppose
. I will
suppose
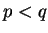 . (Note that if (16.4) holds
when
. (Note that if (16.4) holds
when 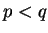 , then it holds when
, then it holds when
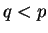 ,
since both sides of the equation change sign when
,
since both sides of the equation change sign when 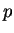 and
and 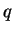 are interchanged.
Also
note that the theorem clearly holds for
are interchanged.
Also
note that the theorem clearly holds for 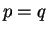 .)
.)
Let
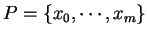 be any partition of
be any partition of ![$[p,q]$](img2569.gif) , and let
, and let 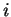 be an
integer
with
be an
integer
with 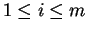 . If
. If 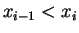 we can apply the mean value theorem to
we can apply the mean value theorem to
 on
on
![$[x_{i-1},x_i]$](img3883.gif) to find a number
to find a number
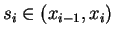 such that
such that
If 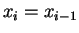 , let
, let 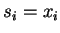 . Then
. Then
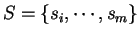 is a sample for
is a sample for
 such that
such that
We have shown that for every partition  of
of ![$[p,q]$](img2569.gif) there is a sample
there is a sample  for
for
 such that
such that
Let 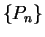 be a sequence of partitions for
be a sequence of partitions for ![$[p,q]$](img2569.gif) such that
such that
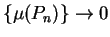 ,
and for each
,
and for each
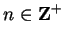 let
let 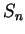 be a sample for
be a sample for 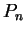 such that
such that
Then, since  is integrable on
is integrable on ![$[q,p]$](img3892.gif) ,
,
16.5
Example.
The fundamental theorem will allow us to evaluate many integrals easily. For
example, we know that
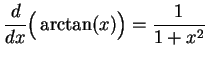
.
Hence, by the fundamental theorem,
This says that the two sets
and
have the same area - a rather remarkable result.
Proof: Since  is continuous on
is continuous on ![$[p,q]$](img2569.gif) we can find numbers
we can find numbers ![$r,s\in [p,q]$](img3901.gif) such
that
such
that
By the inequality theorem for integrals
(here 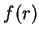 and
and 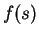 denote constant functions) i.e.,
denote constant functions) i.e.,
i.e.,
We can now apply the intermediate value property to  on the interval whose
endpoints are
on the interval whose
endpoints are 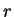 and
and 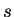 to get a number
to get a number 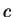 between
between 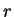 and
and 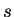 such that
such that
The number 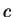 is in the interval
is in the interval 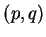 , so we are done.
, so we are done. 
16.8
Exercise.
A
Explain how corollary
16.7 follows
from theorem
16.6. (There is nothing to show unless
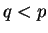
)
Proof: Let ![$t \in [a,b]$](img3911.gif) . I will show that
. I will show that 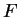 is continuous at
is continuous at  .
Since
.
Since  is integrable on
is integrable on ![$[a,b]$](img1071.gif) there is a number
there is a number 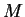 such that
such that
By the corollary to the inequality theorem for integrals (8.17), it
follows
that
for all ![$s,t\in [a,b]$](img3913.gif) . Thus, for all
. Thus, for all ![$s,t\in [a,b]$](img3913.gif) ,
,
Now
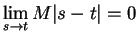 , so by the squeezing rule
for limits of functions,
, so by the squeezing rule
for limits of functions,
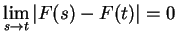 .
It follows that
.
It follows that
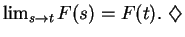 .
.
Proof: Let
and let  be a point in
be a point in  . Let
. Let 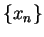 be any sequence in
be any sequence in
![$[a,b]\setminus
\{t\}$](img3921.gif) such that
such that 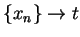 . Then
. Then
By the mean value theorem for integrals, there is a number 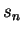 between
between 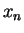 and
and
 such that
such that
Now
and since
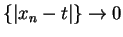 ,
we
have
,
we
have
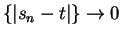 , by the squeezing rule for sequences.
Since
, by the squeezing rule for sequences.
Since  is continuous, we conclude that
is continuous, we conclude that
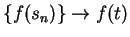 ; i.e.,
; i.e.,
i.e.,
This proves that
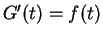 for
for 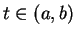 . In addition
. In addition 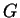 is
continuous
on
is
continuous
on ![$[a,b]$](img1071.gif) by lemma 16.9. Hence
by lemma 16.9. Hence 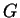 is an antiderivative for
is an antiderivative for  on
on
![$[a,b]$](img1071.gif) .
. 
Remark Leibnitz's
statement of the fundamental principle of the calculus was
the following:
Differences and sums are the inverses of one another, that is
to say, the sum of the differences of a series is a term of the series,
and the difference of the sums of a series is a term of the
series; and I enunciate the former thus, 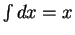 , and the
latter thus,
, and the
latter thus, 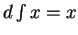 [34, page 142].
[34, page 142].
To see the relation between Leibnitz's formulas and ours, in the equation
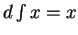 , write
, write 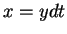 to get
to get
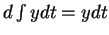 , or
, or
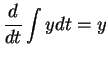 . This corresponds to equation
(16.11). Equation (16.4) can be written as
. This corresponds to equation
(16.11). Equation (16.4) can be written as
If we cancel the 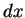 's (in the next chapter we will show that this
is actually justified!) we get
's (in the next chapter we will show that this
is actually justified!) we get
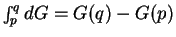 . This is
not quite the same as
. This is
not quite the same as 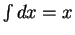 . However if you choose the
origin of coordinates to be
. However if you choose the
origin of coordinates to be 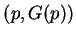 , then the two formulas
coincide.
, then the two formulas
coincide.
To emphasize the inverse-like relation between differentiation and
integration, I will restate our formulas for both parts of the
the fundamental theorem, ignoring all hypotheses:
By exploiting the ambiguous notation for indefinite integrals, we
can get a form almost identical with Leibniz's:
16.12
Example.
Let
We will calculate the derivatives of
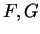
, and
. By the fundamental
theorem,
Now
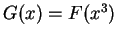
, so by the chain rule,
We have
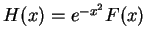
, so by the product rule,
16.13
Exercise.
Calculate the derivatives of the following functions. Simplify your
answers as
much as you can.
- a)
-
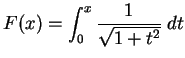
- b)
-
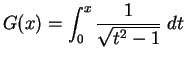
- c)
-
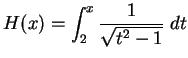
- d)
-
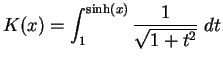
- e)
-
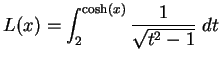 .
.
(We defined
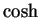
and
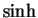
in exercise
14.56.) Find simple
formulas
(not involving any integrals) for
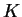
and for
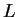
.
A
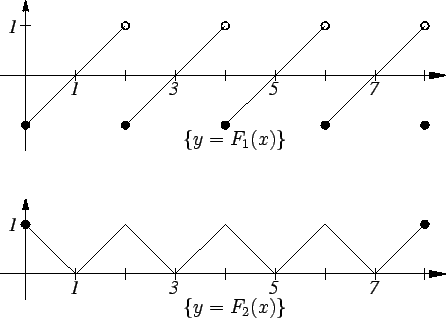
16.15
Exercise.
Let
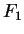
and
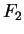
be the functions whose graphs are shown below:
Let
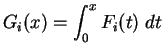
for
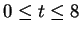
. Sketch the graphs of
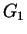
and
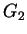
. Include some discussion about why your answer is correct.




Next: 17. Antidifferentiation Techniques
Up: Math 111 Calculus I
Previous: 15.3 Convexity
Index
Ray Mayer
2007-09-07
![]() are
nice. It turns out that every continuous function on
are
nice. It turns out that every continuous function on ![]() is nice, but we
are not
going to prove this. The theorems stated in this chapter for nice functions
are usually stated for continuous functions. You can find a proof that every
continuous
function on an interval
is nice, but we
are not
going to prove this. The theorems stated in this chapter for nice functions
are usually stated for continuous functions. You can find a proof that every
continuous
function on an interval ![]() is integrable on
is integrable on ![]() (and hence that every
continuous function on
(and hence that every
continuous function on ![]() is nice on
is nice on ![]() ) in [44, page 246]
or in
[1, page 153]. However both of these sources use a slightly
different
definition of continuity and of integral than we do, so you will need to do
some work
to translate the proofs in these references into proofs in our terms. You
might try
to prove the result yourself, but the proof is rather tricky. For all the
applications we will make in this course, the functions examined will be
continuous
and piecewise monotonic so the theorems as we prove them are good enough.
) in [44, page 246]
or in
[1, page 153]. However both of these sources use a slightly
different
definition of continuity and of integral than we do, so you will need to do
some work
to translate the proofs in these references into proofs in our terms. You
might try
to prove the result yourself, but the proof is rather tricky. For all the
applications we will make in this course, the functions examined will be
continuous
and piecewise monotonic so the theorems as we prove them are good enough.
![]() is continuous on
is continuous on ![]() and
and
![]() on
on ![]() . Let
. Let ![]() be arbitrary points in
be arbitrary points in ![]() . I will
suppose
. I will
suppose
![]() . (Note that if (16.4) holds
when
. (Note that if (16.4) holds
when ![]() , then it holds when
, then it holds when
![]() ,
since both sides of the equation change sign when
,
since both sides of the equation change sign when ![]() and
and ![]() are interchanged.
Also
note that the theorem clearly holds for
are interchanged.
Also
note that the theorem clearly holds for ![]() .)
.)
![]() be any partition of
be any partition of ![]() , and let
, and let ![]() be an
integer
with
be an
integer
with ![]() . If
. If ![]() we can apply the mean value theorem to
we can apply the mean value theorem to
![]() on
on
![]() to find a number
to find a number
![]() such that
such that
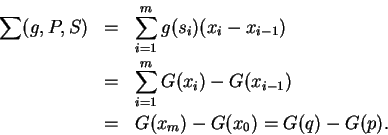
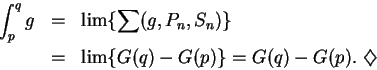
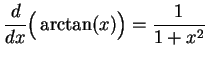 .
Hence, by the fundamental theorem,
.
Hence, by the fundamental theorem,
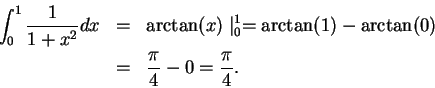
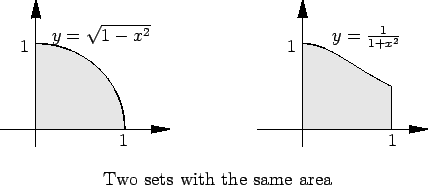
![]() is continuous on
is continuous on ![]() we can find numbers
we can find numbers ![]() such
that
such
that
![]() . I will show that
. I will show that ![]() is continuous at
is continuous at ![]() .
Since
.
Since ![]() is integrable on
is integrable on ![]() there is a number
there is a number ![]() such that
such that
![\begin{eqnarray*}
{{G(x_n)-G(t)}\over {x_n-t}} &=& {1\over {x_n-t}}\Big[
\int_c^{x_n}f-\int_c^tf\Big] \\
&=& {1\over {x_n-t}}\int_t^{x_n}f.
\end{eqnarray*}](img3923.gif)
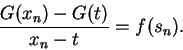
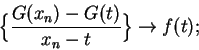
, and the latter thus,
[34, page 142].
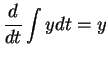 . This corresponds to equation
(16.11). Equation (16.4) can be written as
. This corresponds to equation
(16.11). Equation (16.4) can be written as
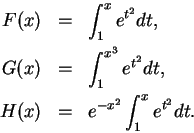
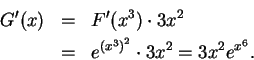
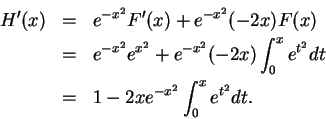
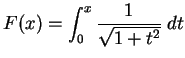
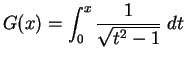
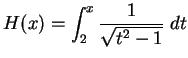
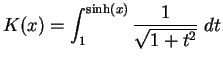
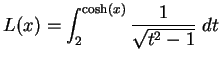 .
.
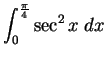 .
.
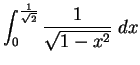 .
.
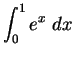 .
.
 for
for