2.2 Some Summation Formulas

We will now develop a formula for the sum

$$1+2+\cdots +n.$$

Figure (a) shows two polygons, each having area $1+2+\cdots +n$. If we slide the two polygons so that they touch, we create a rectangle as in figure (b) whose area is $n(n+1)$. Thus

$$2(1+2+\cdots +n)=n(n+1)$$

i.e.,

$$1+2+\cdots +n={{n(n+1)}\over 2}.$$ (2.8)

The proof just given is quite attractive, and a proof similar to this was probably known to the Pythagoreans in the 6th or 5th centuries B.C. Cf [29, page 30]. The formula itself was known to the Babylonians much earlier than this[45, page 77], but we have no idea how they discovered it.

The idea here is special, and does not generalize to give a formula for $1^2+2^2+\cdots +n^2$. (A nice geometrical proof of the formula for the sum of the first $n$ squares can be found in Proofs Without Words by Roger Nelsen[37, page 77], but it is different enough from the one just given that I would not call it a ``generalization''.) We will now give a second proof of (2.8) that generalizes to give formulas for $1^p+2^p+\cdots +n^p$ for positive integers $p$. The idea we use was introduced by Blaise Pascal [6, page 197] circa 1654.

For any real number $k$, we have

$$(k+1)^2-k^2=k^2+2k+1-k^2=2k+1.$$

Hence

$$\begin{eqnarray*} 1^2-0^2&=&2\cdot 0+1,\\ 2^2-1^2&=&2\cdot 1+1,\\ 3^2-2^2&=&2\cdot 2+1,\\ &\vdots& \\ (n+1)^2 - n^2 &=&2\cdot n+1. \end{eqnarray*}$$

Add the left sides of these $(n+1)$ equations together, and equate the result to the sum of the right sides:

$$(n+1)^2-n^2+\cdots +3^2-2^2+2^2-1^2+1^2-0^2=2\cdot (1+\cdots +n)+(n+1).$$

In the left side of this equation all of the terms except the first cancel. Thus

$$(n+1)^2=2(1+2+\cdots +n)+(n+1)$$

so

$$2(1+2+\cdots +n)=(n+1)^2-(n+1)=(n+1)(n+1-1)=(n+1)n$$

and

$$1+2+\cdots +n={{n(n+1)}\over 2}.$$

This completes the second proof of (2.8).

To find $1^2+2^2+\cdots +n^2$ we use the same sort of argument. For any real number $k$ we have

$$(k+1)^3-k^3=k^3+3k^2+3k+1-k^3=3k^2+3k+1.$$

Hence,

$$\begin{eqnarray*} 1^3-0^3&=&3\cdot 0^2+3\cdot 0+1,\\ 2^3-1^3&=&3\cdot 1^2+3\cdo... ...+3\cdot 2+1,\\ &\vdots&\\ (n+1)^3-n^3&=&3\cdot n^2+3\cdot n+1. \end{eqnarray*}$$

Next we equate the sum of the left sides of these $n+1$ equations with the sum of the right sides. As before, most of the terms on the left side cancel and we obtain

$$(n+1)^3=3(1^2+2^2+\cdots +n^2)+3(1+2+\cdots +n)+(n+1).$$

We now use the known formula for $1+2+3+\cdots +n$:

$$(n+1)^3=3(1^2+2^2+\cdots +n^2)+{3\over 2}n (n+1)+(n+1)$$

so

$$\begin{eqnarray*} 3(1^2+2^2+\cdots +n^2)&=&(n+1)^3-{3\over 2}n(n+1)-(n+1)\\ &=&... ...=(n+1)n\left( n+{1\over 2}\right)\\ &=&{{n(n+1)(2n+1)}\over 2}, \end{eqnarray*}$$

and finally

$$1^2+2^2+\cdots +n^2={{n(n+1)(2n+1)}\over 6}.$$ (2.9)

You should check that this formula agrees with the calculations made in (2.7). The argument we just gave can be used to find formulas for $1^3+2^3+\cdots +n^3$, and for sums of higher powers, but it takes a certain amount of stamina to carry out the details. To find $1^3+2^3+\cdots +n^3$, you could begin with

$$(k+1)^4-k^4=4k^3+6k^2+4k+1 \mbox{ for all } k\in\mbox{{\bf R}}.$$

Add together the results of this equation for $k=0,1,\cdots,n$ and get

$$(n+1)^4=4(1^3+2^3+\cdots +n^3)+6(1^2+2^2+\cdots +n^2)+4(1+\cdots +n)+(n+1).$$

Then use equations (2.8) and (2.9) to eliminate $1^2+2^2+\cdots +n^2$ and $1+\cdots +n$, and solve for $1^3+2^3+\cdots +n^3$.

2.10   Exercise. A Complete the argument started above, and find the formula for $1^3+2^3+\cdots +n^3$.

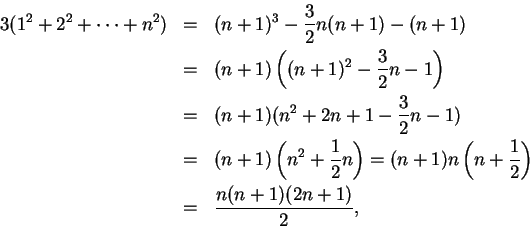
Jacob Bernoulli (1654-1705) considered the general formula for power sums. By using a technique similar to, but slightly different from Pascal's, he constructed the table below. Here $f(1) + f(2) + \cdots f(n)$ is denoted by $\int f(n)$, and $\ast$ denotes a missing term: Thus the $\ast$ in the fourth line of the table below indicates that there is no $n^2$ term, i.e. the coefficient of $n^2$ is zero.

Thus we can step by step reach higher and higher powers and with slight effort form the following table.

Sums of Powers

$$\begin{array}{lllllll} \int n &=\frac{1}{2}nn & +\frac{1}{2}n... ...\frac{1}{2}n^3\ast+\frac{5}{66}n.\mbox{{\nonumber}} \end{array}$$

Whoever will examine the series as to their regularity may be able to continue the table[9, pages 317-320]. ^2.1

He then states a rule for continuing the table. The rule is not quite an explicit formula, rather it tells how to compute the next line easily when the previous lines are known.

2.11   Entertainment (Bernoulli's problem.) Guess a way to continue the table. Your answer should be explicit enough so that you can actually calculate the next two lines of the table.

A formula for $1^2+2^2+\cdots +n^2$ was proved by Archimedes (287-212 B.C.). (See Archimedes On Conoids and Spheroids in [2, pages 107-109]). The formula was known to the Babylonians[45, page 77] much earlier than this in the form

$$1^2 + 2^2 + \cdots + n^2 = \big( {1\over 3} + n \cdot {2 \over 3} \big) ( 1 + 2 + \cdots + n).$$

A technique for calculating general power sums has been known since circa 1000 A.D. At about this time Ibn-al-Haitham, gave a method based on the picture below, and used it to calculate the power sums up to $1^4 + 2^4 + \cdots + n^4$. The method is discussed in [6, pages 66-69]