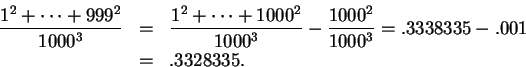Next: 2.2 Some Summation Formulas
Up: 2. Some Area Calculations
Previous: 2. Some Area Calculations
Index
2.1 The Area Under a Power Function
Let  be a positive number, let
be a positive number, let 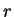 be a positive number,
and let
be a positive number,
and let 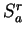 be the set of points
be the set of points 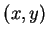 in
in
 such that
such that 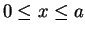 and
and
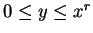 . In this section we will
begin an investigation of the area of
. In this section we will
begin an investigation of the area of 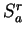 .
.
Our discussion will not apply to negative values of 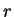 ,
since we make frequent use of the fact that for all non-negative
numbers
,
since we make frequent use of the fact that for all non-negative
numbers  and
and 
Also 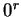 is not defined when
is not defined when 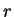 is negative.
is negative.
The figures for the argument given below are for the case 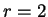 ,
but you should observe
that the proof does not depend on the pictures.
,
but you should observe
that the proof does not depend on the pictures.
Let  be a positive integer, and for
be a positive integer, and for
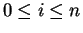 , let
, let
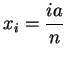 .
.
Then
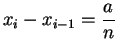 for
for 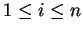 , so the points
, so the points 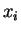 divide
the interval
divide
the interval ![$[0,a]$](img190.gif) into
into  equal subintervals. For
equal subintervals. For 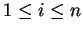 , let
, let
If
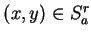 , then
, then
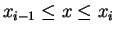 for some index
for some index 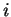 , and
, and
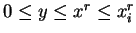 , so
, so
Hence we have
and thus
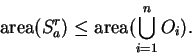 |
(2.1) |
If 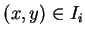 , then
, then
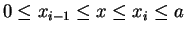 and
and
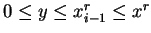 so
so
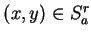 . Hence,
. Hence,
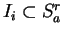 for all
for all 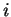 , and
hence
, and
hence
so that
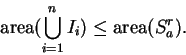 |
(2.2) |
Now
and
Since the boxes 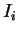 intersect only along their boundaries, we have
intersect only along their boundaries, we have
and similarly
Thus it follows from equations (2.1) and (2.2) that
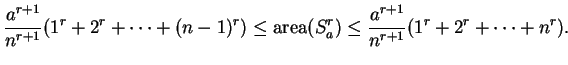 |
|
|
(2.4) |
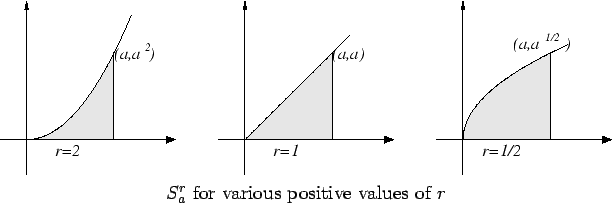
The geometrical question of finding the area of 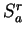 has led us
to the numerical problem of finding the sum
has led us
to the numerical problem of finding the sum
We will study this problem in the next section.
2.5
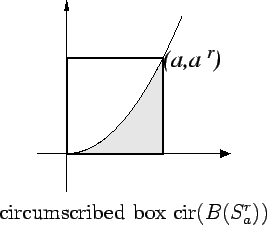
Definition (Circumscribed box.)
Let
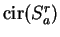
be the smallest box containing

. i.e.
Notice that
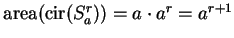 . Thus equation
(2.4) can be written as
. Thus equation
(2.4) can be written as
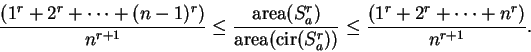 |
(2.6) |
Observe that the outside terms in (2.6) do not depend on  .
.
Now we will specialize to the case when 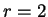 .
A direct calculation shows that
.
A direct calculation shows that
There is a simple (?) formula for
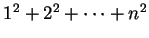 , but it is not
particularly easy to guess this formula on the basis of these calculations.
With
the help of my computer, I checked that
, but it is not
particularly easy to guess this formula on the basis of these calculations.
With
the help of my computer, I checked that
Also
Thus by taking 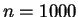 in equation (2.6) we see that
in equation (2.6) we see that
On the basis of the computer evidence it is very tempting to guess that




Next: 2.2 Some Summation Formulas
Up: 2. Some Area Calculations
Previous: 2. Some Area Calculations
Index
Ray Mayer
2007-09-07

![]() ,
since we make frequent use of the fact that for all non-negative
numbers
,
since we make frequent use of the fact that for all non-negative
numbers ![]() and
and ![]()
![]() ,
but you should observe
that the proof does not depend on the pictures.
,
but you should observe
that the proof does not depend on the pictures.
![]() be a positive integer, and for
be a positive integer, and for
![]() , let
, let
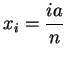 .
.
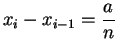 for
for ![]() , so the points
, so the points ![]() divide
the interval
divide
the interval ![]() into
into ![]() equal subintervals. For
equal subintervals. For ![]() , let
, let
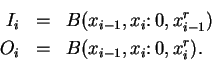
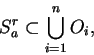
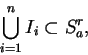
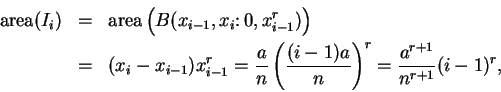
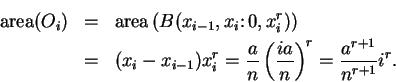
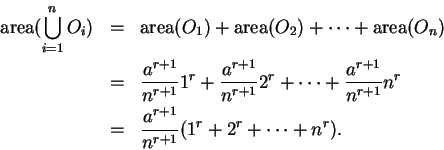
![]() has led us
to the numerical problem of finding the sum
has led us
to the numerical problem of finding the sum
![]() . Thus equation
(2.4) can be written as
. Thus equation
(2.4) can be written as
![]() .
A direct calculation shows that
.
A direct calculation shows that