



Next: 14.6 Some Derivative Calculations
Up: 14. The Inverse Function
Previous: 14.4 The Exponential Function
Index
14.38
Lemma.
Let  be a strictly increasing continuous function whose domain is
an interval
be a strictly increasing continuous function whose domain is
an interval ![$[a,b]$](img1071.gif) . Then the image of
. Then the image of  is the interval
is the interval
![$[f(a),f(b)]$](img3602.gif) , and the function
, and the function
![$f:[a,b] \to [f(a),f(b)]$](img3603.gif) has an inverse.
has an inverse.
Proof: It is clear that 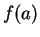 and
and 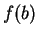 are in image
are in image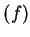 .
Since
.
Since  is continuous we can apply the intermediate value property
to conclude that for every number
is continuous we can apply the intermediate value property
to conclude that for every number 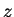 between
between 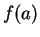 and
and 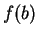 there is a number
there is a number ![$c \in [a,b]$](img2104.gif) such that
such that 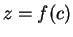 ,
i.e.
,
i.e.
![$[f(a),f(b)] \subset $](img3605.gif) image
image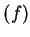 . Since
. Since  is increasing
on
is increasing
on ![$[a,b]$](img1071.gif) we have
we have
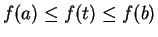 whenever
whenever
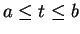 ,
and thus image
,
and thus image
![$(f) \subset [f(a),f(b)]$](img3608.gif) . It follows that
. It follows that
![$f:[a,b] \to [f(a),f(b)]$](img3603.gif) is surjective, and since strictly increasing
functions are injective,
is surjective, and since strictly increasing
functions are injective,  is bijective. By remark (14.22)
is bijective. By remark (14.22)
 has an inverse.
has an inverse.
14.39
Exercise.
State and prove the analogue of lemma
14.38
for strictly decreasing functions.
14.40
Exercise.
Let

be a function whose domain
is an interval
![$[a,b]$](img1071.gif)
, and whose image is an interval. Does it
follow that

is continuous?
14.41
Exercise.
A
Let

be a continuous function on a
closed bounded interval
![$[a,b]$](img1071.gif)
. Show that the image of

is a closed bounded interval
![$[A,B]$](img3609.gif)
.
14.42
Exercise.
Let

and
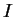
be non-empty intervals and let
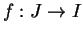
be a
continuous function such that
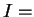
image(

).
a) Show that if  is strictly increasing, then the inverse function
for
is strictly increasing, then the inverse function
for  is also strictly increasing.
is also strictly increasing.
b) Show that if  is strictly decreasing, then the inverse function for
is strictly decreasing, then the inverse function for
 is also strictly decreasing.
is also strictly decreasing.
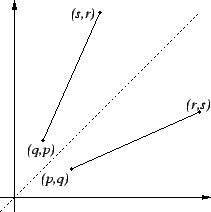
Remark:
If 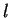 is a nonvertical line joining two points
is a nonvertical line joining two points 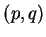 and
and 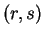 then the slope of
then the slope of 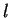 is
is
The reflection of 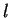 about the line whose equation is
about the line whose equation is 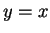 passes
through the points
passes
through the points 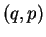 and
and 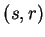 , so the slope of the reflected
line is
, so the slope of the reflected
line is
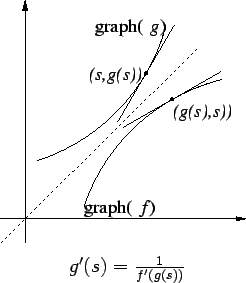
Thus theorem 14.43 says that the tangent to graph( ) at the
point
) at the
point 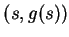 is obtained by reflecting the tangent to graph(
is obtained by reflecting the tangent to graph( )
at
)
at 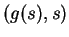 about the line whose equation is
about the line whose equation is 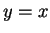 . This is what you should
expect from
the geometry of the situation.
. This is what you should
expect from
the geometry of the situation.
Proof of theorem 14.43:
The first thing that should be done, is to prove that  is continuous.
I am going to omit that proof and just assume the continuity of
is continuous.
I am going to omit that proof and just assume the continuity of  ,
and then show that
,
and then show that  is differentiable,
and that
is differentiable,
and that 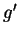 is given by formula (14.44).
is given by formula (14.44).
Let 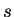 be a point
in the interior of
be a point
in the interior of
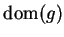 . then
. then
(Observe that we have not divided by zero). Let 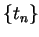 be a sequence in
be a sequence in
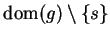 such that
such that 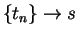 .
Then
.
Then
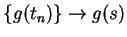 (since
(since  is assumed to be
continuous), and
is assumed to be
continuous), and
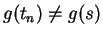 for all
for all
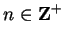 (since
(since  is injective). Since
is injective). Since  is differentiable
at
is differentiable
at 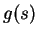 , it follows that
, it follows that
Since
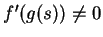 it follows that
it follows that
It follows that
and the theorem is proved. 
Remark: The inverse function theorem also applies to continuous
functions  on
on  such that
such that 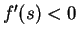 for all
for all 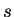 in interior
in interior  .
Formula (14.44) is valid in this case also.
.
Formula (14.44) is valid in this case also.
Remark: Although we have stated the inverse function
theorem for functions on intervals of the form ![$[a,b]$](img1071.gif) , it holds for
functions defined on any interval. Let
, it holds for
functions defined on any interval. Let  be an interval, and let
be an interval, and let  be a continuous strictly increasing function from
be a continuous strictly increasing function from  to R such that
to R such that
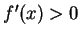 for all
for all  in the interior of
in the interior of  . Let
. Let 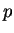 be a point
in the interior of image
be a point
in the interior of image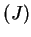 . Then we can find points
. Then we can find points 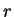 and
and 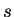 in image
in image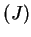 such that
such that 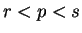 . Now
. Now  maps the interval
maps the interval
![$[g(r),g(s)]$](img3643.gif) bijectively onto
bijectively onto ![$[r,s]$](img3644.gif) , and since
, and since 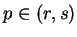 we can apply the inverse function theorem on the interval
we can apply the inverse function theorem on the interval ![$[g(r),g(s)]$](img3643.gif) to conclude that
to conclude that
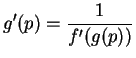 . It is not necessary
to remember the formula for
. It is not necessary
to remember the formula for 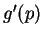 . Once we know that
. Once we know that  is
differentiable, we can calculate
is
differentiable, we can calculate 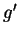 by using the chain rule, as illustrated
by the examples in the next section.
by using the chain rule, as illustrated
by the examples in the next section.




Next: 14.6 Some Derivative Calculations
Up: 14. The Inverse Function
Previous: 14.4 The Exponential Function
Index
Ray Mayer
2007-09-07
![]() is strictly increasing, then the inverse function
for
is strictly increasing, then the inverse function
for ![]() is also strictly increasing.
is also strictly increasing.
![]() is strictly decreasing, then the inverse function for
is strictly decreasing, then the inverse function for
![]() is also strictly decreasing.
is also strictly decreasing.
![]() is a nonvertical line joining two points
is a nonvertical line joining two points ![]() and
and ![]() then the slope of
then the slope of ![]() is
is
![]() is continuous.
I am going to omit that proof and just assume the continuity of
is continuous.
I am going to omit that proof and just assume the continuity of ![]() ,
and then show that
,
and then show that ![]() is differentiable,
and that
is differentiable,
and that ![]() is given by formula (14.44).
is given by formula (14.44).
![]() be a point
in the interior of
be a point
in the interior of
![]() . then
. then
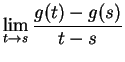
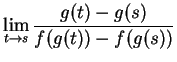
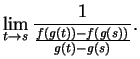
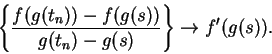
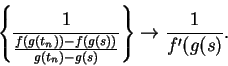
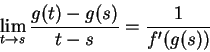
![]() on
on ![]() such that
such that ![]() for all
for all ![]() in interior
in interior ![]() .
Formula (14.44) is valid in this case also.
.
Formula (14.44) is valid in this case also.
![]() , it holds for
functions defined on any interval. Let
, it holds for
functions defined on any interval. Let ![]() be an interval, and let
be an interval, and let ![]() be a continuous strictly increasing function from
be a continuous strictly increasing function from ![]() to R such that
to R such that
![]() for all
for all ![]() in the interior of
in the interior of ![]() . Let
. Let ![]() be a point
in the interior of image
be a point
in the interior of image![]() . Then we can find points
. Then we can find points ![]() and
and ![]() in image
in image![]() such that
such that ![]() . Now
. Now ![]() maps the interval
maps the interval
![]() bijectively onto
bijectively onto ![]() , and since
, and since ![]() we can apply the inverse function theorem on the interval
we can apply the inverse function theorem on the interval ![]() to conclude that
to conclude that
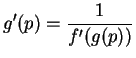 . It is not necessary
to remember the formula for
. It is not necessary
to remember the formula for ![]() . Once we know that
. Once we know that ![]() is
differentiable, we can calculate
is
differentiable, we can calculate ![]() by using the chain rule, as illustrated
by the examples in the next section.
by using the chain rule, as illustrated
by the examples in the next section.