



Next: 14.5 Inverse Function Theorems
Up: 14. The Inverse Function
Previous: 14.3 Inverse Functions
Index
14.29
Example.
We will now derive some properties of the
inverse function
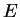
of the logarithm.
We have
For all  and
and  in R,
in R,
If we apply
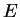
to both sides of this equality we get
For all
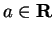
we have
from which it follows that
If
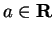
and
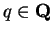
we have
If we apply
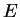
to both sides of this identity we get
In particular,
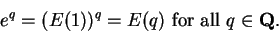 |
(14.30) |
Now we have defined 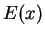 for all
for all
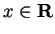 , but we have only defined
, but we have only defined
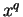 when
when
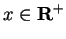 and
and
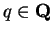 . (We know what
. (We know what
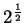 is,
but we have not defined
is,
but we have not defined 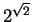 .)
Because of relation (14.30) we often write
.)
Because of relation (14.30) we often write 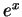 in place of
in place of 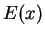 .
.
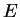 is
called the exponential function, and is written
is
called the exponential function, and is written
We can summarize the results of this example in the following theorem:
14.31
Theorem (Properties of the exponential function.) The exponential function is a function from R onto
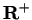 .
We have
.
We have
Proof: We have proved all of these properties except
for relation (14.32). The proof of (14.32)
is the next exercise.
14.34
Exercise.
Show that
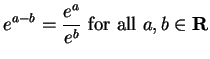
.
14.35
Exercise.
Show that if
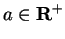
and
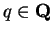
, then
14.36
Definition (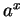 .)
.)
The result of the
last exercise motivates us to make the definition
14.37
Exercise.
Prove the following results:




Next: 14.5 Inverse Function Theorems
Up: 14. The Inverse Function
Previous: 14.3 Inverse Functions
Index
Ray Mayer
2007-09-07
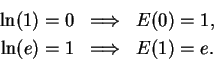
![]() and
and ![]() in R,
in R,
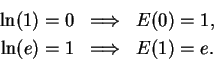
![]() and
and ![]() in R,
in R,
![]() for all
for all
![]() , but we have only defined
, but we have only defined
![]() when
when
![]() and
and
![]() . (We know what
. (We know what
![]() is,
but we have not defined
is,
but we have not defined ![]() .)
Because of relation (14.30) we often write
.)
Because of relation (14.30) we often write ![]() in place of
in place of ![]() .
.
![]() is
called the exponential function, and is written
is
called the exponential function, and is written
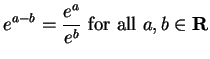 .
.