



Next: 14.4 The Exponential Function
Up: 14. The Inverse Function
Previous: 14.2 Applications
Index
14.12
Definition (Injective.)
Let

and
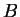
be sets. A function
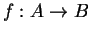
is called
injective
or
one-to-one if and only if for all points
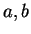
in

or equivalently if and only if
If

is a function whose domain and codomain are subsets of
R then

is injective if and only if each horizontal line
intersects the graph of

at most once.
14.13
Examples.
Let
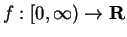
and
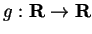
be defined by
Then

is injective, since for all
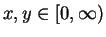
we have
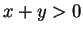
,
and hence
However

is not injective, since
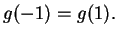
14.14
Remark (Strictly monotonic functions are injective.)
If
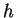
is strictly increasing on an interval

, then
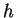
is injective on

,
since for all
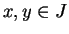
Similarly, any strictly decreasing function on

is injective.
14.15
Definition (Surjective.)
Let
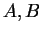
be sets and let
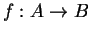
. We say that

is
surjective if and only if
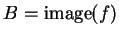
, i.e. if and only if for every
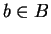
there
is at least one element

of

such that
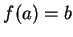
.
14.16
Examples.
Let
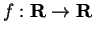
and
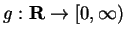
be defined by
Then

is surjective, since if
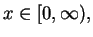
then
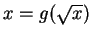
, but

is not surjective, since
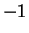
is not
in the image of

.
14.18
Definition (Bijective.)
Let
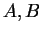
be sets. A function
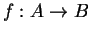
is called
bijective if and only if

is both injective and surjective.
14.20
Remark.
Let

and
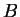
be sets, and let
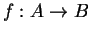
be a bijective function.
Let

be a generic element of
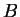
. Since

is surjective, there is an element

in

such that
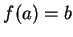
. Since

is injective this element

is unique, i.e. if

and
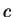
are elements of

then
Hence we can define a function
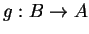
by the rule
Then by definition
Now let
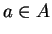
, so that
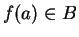
. It is clear that the
unique
element
in

such that
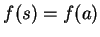
is
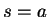
, and hence
14.21
Definition (Inverse function.)
Let
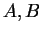
be sets, and let
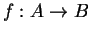
. An
inverse function for

is a function
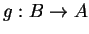
such that
14.22
Remark (Bijective functions have inverses.)
Notice that in the definition of inverse functions, both the domain
and the codomain of

enter in a crucial way.
It is clear that if

is an inverse function for

, then

is an
inverse function for

.
Remark
14.20
shows that every bijective function
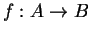
has an inverse.
14.23
Example.
Let
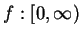
be defined by
We saw above that

is bijective, and hence has an inverse. If
Then it is clear that

is an inverse function for

.
We also saw that
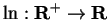 is bijective, and so it
has an inverse. This inverse is not expressible in terms
of any functions we have discussed. We will give it a name.
is bijective, and so it
has an inverse. This inverse is not expressible in terms
of any functions we have discussed. We will give it a name.
14.24
Definition (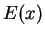 .)
.)
Let
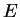
denote the inverse of the logarithm
function. Thus
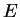
is a function from
R to
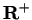
, and it
satisfies the conditions
We will investigate the properties of
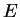
after we have proved a few general
properties of inverse functions.
In order to speak of the inverse of a function, as we did in the last
definition, we should note that inverses are unique.
14.25
Theorem (Uniqueness of inverses.) Let 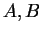 be sets and let
be sets and let
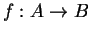 . If
. If  and
and 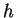 are inverse functions for
are inverse functions for  , then
, then 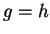 .
.
Proof: If  and
and 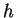 are inverse functions for
are inverse functions for  then
then
and
Also for all 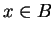
(I have used the facts that 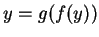 for all
for all 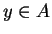 , and
, and 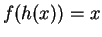 for all
for all 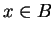 ).
).
14.26
Theorem (Reflection theorem.) Let 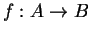 be a function which has
an inverse function
be a function which has
an inverse function 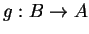 . Then for all
. Then for all
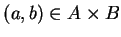
Proof: Let 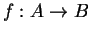 be a function that has an inverse function
be a function that has an inverse function
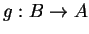 . Then for all
. Then for all
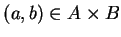
and
Thus
Now
and
and the theorem now follows. 
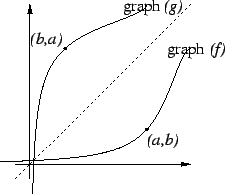
Remark: If  is a bijective function with
is a bijective function with
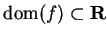 and codomain(
and codomain( )
)
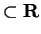 Then the reflection theorem says that if
Then the reflection theorem says that if  is the
inverse function for
is the
inverse function for  , then graph(
, then graph( ) =
) = 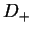 (graph
(graph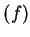 )
where
)
where 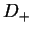 is the reflection about the line
is the reflection about the line 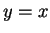 .
.
Since we know what the graph of 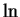 looks like, we can
make a reasonable sketch of graph
looks like, we can
make a reasonable sketch of graph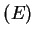 .
.
It is a standard notation to denote the inverse of a function  by
by 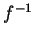 .
However since this is also a standard notation for the function
.
However since this is also a standard notation for the function
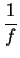 which is an entirely different object,
I will not use this notation.
which is an entirely different object,
I will not use this notation.
We have shown that if 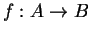 is bijective, then
is bijective, then  has an inverse
function. The converse is also true.
has an inverse
function. The converse is also true.
14.27
Theorem.
Let 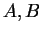 be sets and let
be sets and let 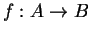 . If
. If  has an inverse
function, then
has an inverse
function, then  is both injective and surjective.
is both injective and surjective.
Proof: Suppose  has an inverse function
has an inverse function 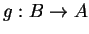 . Then for
all
. Then for
all 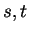 in
in  we have
we have
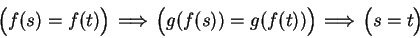 |
(14.28) |
and hence  is injective. Also, for each
is injective. Also, for each 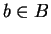
so 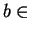 image(
image( ), and
), and  is surjective.
is surjective. 




Next: 14.4 The Exponential Function
Up: 14. The Inverse Function
Previous: 14.2 Applications
Index
Ray Mayer
2007-09-07
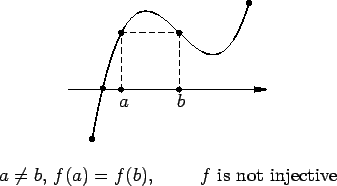
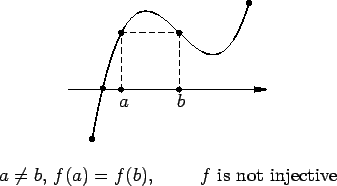
![]() ,
, ![]() is injective and surjective.
is injective and surjective.
![]() ,
, ![]() is injective but not surjective.
is injective but not surjective.
![]() ,
, ![]() is surjective but not injective.
is surjective but not injective.
![]() ,
, ![]() is neither injective nor surjective.
is neither injective nor surjective.
![]() is a bijective function from
is a bijective function from
![]() to R.
We know that ln is strictly increasing, and hence is injective.
If
to R.
We know that ln is strictly increasing, and hence is injective.
If ![]() is any real number we know that
is any real number we know that ![]() takes on
values greater than
takes on
values greater than ![]() , and values less that
, and values less that ![]() , so by the
intermediate value property (here we use the fact that
, so by the
intermediate value property (here we use the fact that ![]() is
continuous) it also takes on the value
is
continuous) it also takes on the value ![]() , i.e.
, i.e.
![]() is surjective.
is surjective.
![]() is bijective, and so it
has an inverse. This inverse is not expressible in terms
of any functions we have discussed. We will give it a name.
is bijective, and so it
has an inverse. This inverse is not expressible in terms
of any functions we have discussed. We will give it a name.
![]() is a bijective function with
is a bijective function with
![]() and codomain(
and codomain(![]() )
)
![]() Then the reflection theorem says that if
Then the reflection theorem says that if ![]() is the
inverse function for
is the
inverse function for ![]() , then graph(
, then graph(![]() ) =
) = ![]() (graph
(graph![]() )
where
)
where ![]() is the reflection about the line
is the reflection about the line ![]() .
.
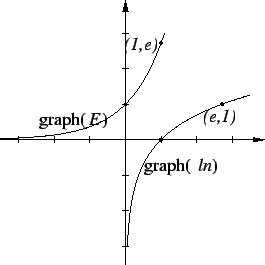
![]() by
by ![]() .
However since this is also a standard notation for the function
.
However since this is also a standard notation for the function
![]() which is an entirely different object,
I will not use this notation.
which is an entirely different object,
I will not use this notation.
![]() is bijective, then
is bijective, then ![]() has an inverse
function. The converse is also true.
has an inverse
function. The converse is also true.