



Next: 17.2 Basic Formulas
Up: 17. Antidifferentiation Techniques
Previous: 17. Antidifferentiation Techniques
Index
17.1
Definition (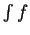 or
or 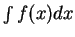 .)
.)
I am going to use the notation
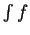
or
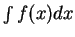
to
denote some arbitrary antiderivative for

on an
interval that often will not be specified. This is
the same notation that I used previously to denote
an indefinite integral for

.
Although the fundamental
theorem of the calculus shows that for nice functions the
concepts of ``antiderivative'' and ``indefinite integral'' are
essentially the same, for arbitrary functions the two concepts
do not coincide. For example, let
Then

has an indefinite integral
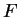
where
Thus
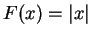
. Then
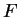
is not an antiderivative for

, since
we know that
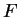
is not differentiable at 0.
I will always try to make it clear whether 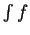 represents
an antiderivative or an indefinite integral in cases where
it makes a difference.
represents
an antiderivative or an indefinite integral in cases where
it makes a difference.
The problem of calculating derivatives is straightforward. By using
known formulas and rules, you can easily find the derivative of
almost any function you can write down. The problem of calculating
antiderivatives is much more complicated. In fact, none of the five functions
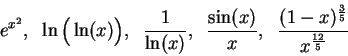 |
(17.2) |
have antiderivatives that can be expressed in terms of functions we have
studied. (To find a proof of this assertion, see [40, page 37 ff]
and [41].) The
first two functions in this list are compositions of functions that have simple
antiderivatives, the third function is the reciprocal of a function with a
simple antiderivative, and each of the last two functions is a product
of two functions with
simple antiderivatives. (An antiderivative for 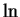 will be calculated in
(17.25).) It follows that there is no chain rule or reciprocal rule or
product rule for calculating antiderivatives. We will see, however, that the
chain rule and the product rule for differentiation do give rise to
antidifferentiation formulas.
will be calculated in
(17.25).) It follows that there is no chain rule or reciprocal rule or
product rule for calculating antiderivatives. We will see, however, that the
chain rule and the product rule for differentiation do give rise to
antidifferentiation formulas.
The five functions
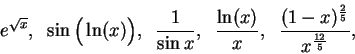 |
(17.3) |
which look somewhat similar to the functions in (17.2),
turn out to
have simple antiderivatives, as you will see in
(17.42c),
(17.22),
(17.7),
(17.31f),
and (17.41). It is often not easy
to tell the difference between a function that has a simple
antiderivative and a function that does not.
Many simple functions that arise in applied problems do not have simple
antiderivatives. The exercises in this chapter have been carefully designed to
be non-typical functions whose antiderivatives can be found.
The Maple instructions for finding antiderivatives and integrals are
and
I gave the five functions in (17.2) to Maple
to antidifferentiate.
The results were:
> int( exp(x^2),x);
> int( ln(ln(x)),x);
> int(1/ln(x),x);
> int(sin(x)/x,x);
> int( ((1-x)^(3/5))/ (x^(12/5)),x);
In the first four cases, an answer has been given involving names of
functions we have
not seen before, (and which we will not see again in this course). The
definitions of these functions are:
In equation (17.4), we assume that
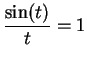 when
when
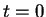 . The function Si is called the sine integral.
In equation (17.5),
Ei
. The function Si is called the sine integral.
In equation (17.5),
Ei makes sense only when
makes sense only when  is
positive. The definition of Ei
is
positive. The definition of Ei for
for 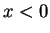 involves ideas we have not
discussed. The function Ei is called the exponential integral.
involves ideas we have not
discussed. The function Ei is called the exponential integral.
The
function erf is called the error function. The answer given by
Maple for
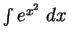 involves the
symbol
involves the
symbol 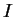 .
This is Maple's notation for
.
This is Maple's notation for 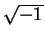 . The definition of erf
. The definition of erf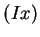 makes
no sense in terms of concepts we have studied. However you can use Maple
to calculate integrals even if you do not know what the symbols mean.
The following instructions find
makes
no sense in terms of concepts we have studied. However you can use Maple
to calculate integrals even if you do not know what the symbols mean.
The following instructions find
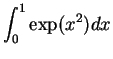 :
:
> int( exp(x^2),x= 0..1);
> evalf(%);




Next: 17.2 Basic Formulas
Up: 17. Antidifferentiation Techniques
Previous: 17. Antidifferentiation Techniques
Index
Ray Mayer
2007-09-07
![]() represents
an antiderivative or an indefinite integral in cases where
it makes a difference.
represents
an antiderivative or an indefinite integral in cases where
it makes a difference.
![]() represents
an antiderivative or an indefinite integral in cases where
it makes a difference.
represents
an antiderivative or an indefinite integral in cases where
it makes a difference.
![\begin{displaymath}-{\frac {5}{14}}
{\frac {2-5 x+3 {x}^{2}}{x\sqrt [5]{ \le...
...4 {\frac {1}{\sqrt [5]{ \left( -1+x \right) ^{2}{x}^{2}}}}{dx}\end{displaymath}](img3977.gif)
 when
when
![]() involves the
symbol
involves the
symbol ![]() .
This is Maple's notation for
.
This is Maple's notation for ![]() . The definition of erf
. The definition of erf![]() makes
no sense in terms of concepts we have studied. However you can use Maple
to calculate integrals even if you do not know what the symbols mean.
The following instructions find
makes
no sense in terms of concepts we have studied. However you can use Maple
to calculate integrals even if you do not know what the symbols mean.
The following instructions find
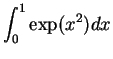 :
: