We call formula (17.18) the formula for integration by parts.
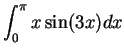 .
We begin by
searching for an antiderivative for
.
We begin by
searching for an antiderivative for 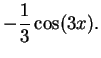 |
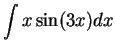 |
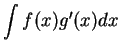 |
||
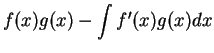 |
|||
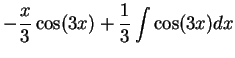 |
|||
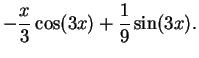 |
(17.20) |
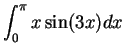 |
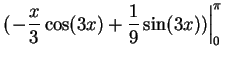 |
||
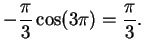 |
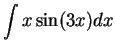 |
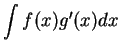 |
||
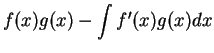 |
|||
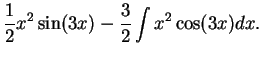 |
(17.21) |
Integration by parts is used to evaluate antiderivatives of the
forms
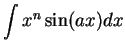 ,
,
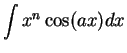 ,
and
,
and
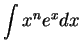 when
when ![]() is a positive integer. These can be reduced to antiderivatives
of the forms
is a positive integer. These can be reduced to antiderivatives
of the forms
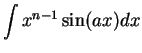 ,
,
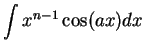 ,
and
,
and
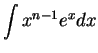 , so by applying the process
, so by applying the process ![]() times we get
the power of
times we get
the power of ![]() down to
down to ![]() , which gives us antiderivatives
we can easily find.
, which gives us antiderivatives
we can easily find.
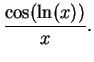 |
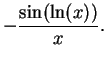 |
Proof: Let ![]() . Then
. Then ![]() , and
, and
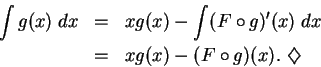
Remark: It follows from the proof of the previous theorem that
if
you know an antiderivative for a function ![]() , then you can find an
antiderivative
for the inverse function
, then you can find an
antiderivative
for the inverse function ![]() by integration by parts. This is what you should
remember about the theorem. The formula (17.27) is not very
memorable.
by integration by parts. This is what you should
remember about the theorem. The formula (17.27) is not very
memorable.
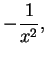 |
|||
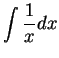 |
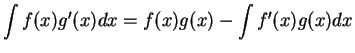 |
||
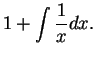 |
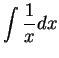 from both sides we obtain
from both sides we obtain
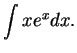
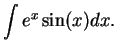 (Integrate by parts more than once.)
(Integrate by parts more than once.)
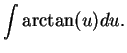
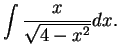
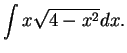
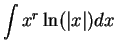 , where
, where
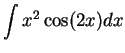 .
.