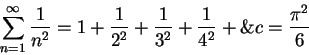
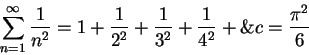
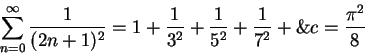
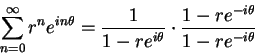
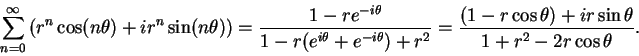
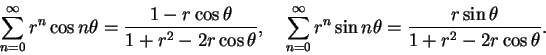
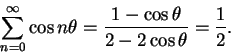
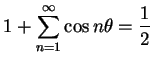 , so
, so
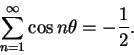
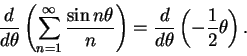
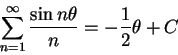
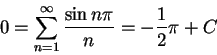
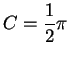 and thus
and thus
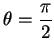 , this gives us
, this gives us
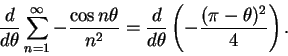
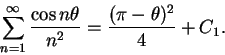
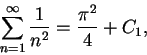
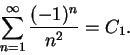
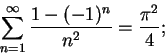
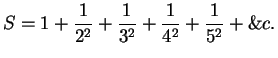 Subtract (12.80) from this to get
Subtract (12.80) from this to get
![\begin{eqnarray*}
S-{{\pi^2}\over 8}&=&{1\over {2^2}}+{1\over {4^2}}+{1\over {6^...
...4}\left[1+{1\over {2^2}}+{1\over {3^2}}+\&c \right]={1\over 4}S.
\end{eqnarray*}](img2206.gif)
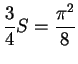 , and then
, and then
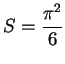 .
.
An argument similar to the following was given by Jacob Bernoulli in 1689
[31, p 443]. Let
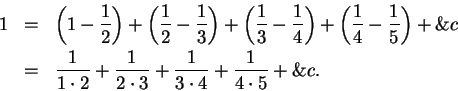
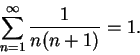
Pi
The notation ![]() was introduced by Euler in 1727 or 1728
to denote the base of natural logarithms[15, vol 2, p 13].
In Mathematica
was introduced by Euler in 1727 or 1728
to denote the base of natural logarithms[15, vol 2, p 13].
In Mathematica ![]() is denoted by
is denoted by E![]() . In the current
version of Maple there is no special name for
. In the current
version of Maple there is no special name for ![]() ; it is denoted
by
; it is denoted
by exp(1)![]() .
.