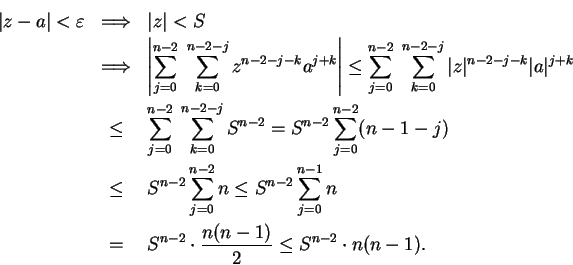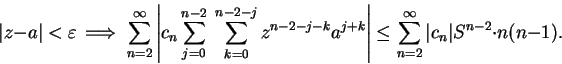Next: 12.9 Some XVIII-th Century
Up: 12. Power Series
Previous: 12.7 Special Values of
Index
12.8 Proof of the Differentiation Theorem
12.73
Lemma.
The power series 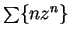 has
radius of convergence equal to
has
radius of convergence equal to  .
.
12.74
Exercise.
Prove lemma
12.73. (We proved this lemma earlier using the differentiation
theorem. Since we need this result to prove the differentiation theorem,
we now want a proof that does
not use the differentiation theorem.)
12.75
Lemma.
Let
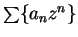 be a power series. Then the two series
be a power series. Then the two series
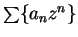 and
and
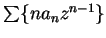 have the same radius of convergence.
have the same radius of convergence.
Proof: I'll show that for all
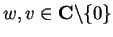 .
.
- a) If
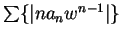 converges, then
converges, then
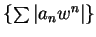 converges.
converges.
- b) If
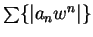 converges and
converges and 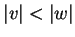 , then
, then
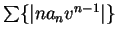 converges.
converges.
a) follows from the comparison test, since
To prove b), suppose
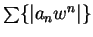 converges and
converges and 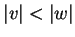 . By lemma
12.73,
. By lemma
12.73,
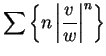 converges, and
hence
converges, and
hence
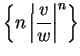 is bounded. Choose
is bounded. Choose
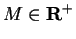 such that
such that
Then 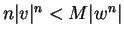 , and
, and
By the comparison test,
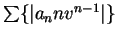 converges.
converges.

12.76
Corollary.
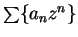 and
and
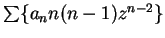 have the same radius of convergence.
have the same radius of convergence.
Proof: Use the lemma twice.

12.77
Theorem.
Let
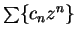 be a power series with positive radius of convergence. Let
be a power series with positive radius of convergence. Let
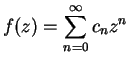 for all
for all 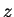 in the disc of convergence for
in the disc of convergence for  and let
and let
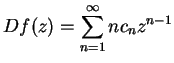 be the function corresponding to
the formal derivative of
be the function corresponding to
the formal derivative of
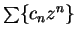 . Then
. Then  is differentiable on its disc
of convergence, and
is differentiable on its disc
of convergence, and 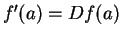 for all
for all  in the disc of convergence.
in the disc of convergence.
Proof: Let  be a point in the disc of convergence, and let
be a point in the disc of convergence, and let 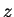 be a different
point in the disc. Then
be a different
point in the disc. Then
Let
Then
and since
the theorem will follow if we can show that 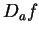 is continuous at
is continuous at  .
.
In the calculation below, I quietly use the following facts:
- a) When
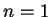 ,
,
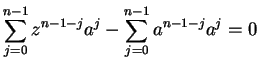 .
.
- b) When
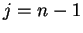 ,
,
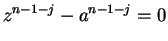 .
.
Let the radius of convergence of our power series be 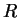 , and let
, and let
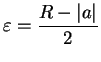 . Then
. Then
Let
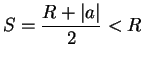 . Then
. Then 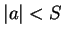 , and
, and
(Here I've used the fact that 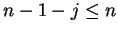 for
for
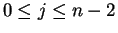 .) Thus
.) Thus
We noticed in the corollary to lemma 12.75 that the series
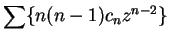 has radius of convergence
has radius of convergence 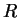 , and hence
, and hence
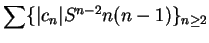 converges to a limit
converges to a limit 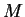 , and by
(12.78),
, and by
(12.78),
If 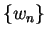 is a sequence in
is a sequence in
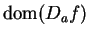 such that
such that 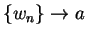 , then
, then
for all large 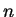 , and by the
null-times bounded theorem and comparison theorem for null sequences,
, and by the
null-times bounded theorem and comparison theorem for null sequences,
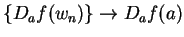 . Hence,
. Hence, 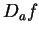 is continuous at
is continuous at  .
.





Next: 12.9 Some XVIII-th Century
Up: 12. Power Series
Previous: 12.7 Special Values of
Index
![]() .
.
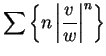 converges, and
hence
converges, and
hence
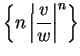 is bounded. Choose
is bounded. Choose
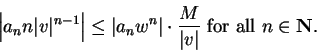
![]()
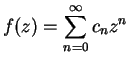 for all
for all 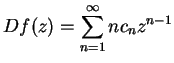 be the function corresponding to
the formal derivative of
be the function corresponding to
the formal derivative of
![]() be a point in the disc of convergence, and let
be a point in the disc of convergence, and let ![]() be a different
point in the disc. Then
be a different
point in the disc. Then
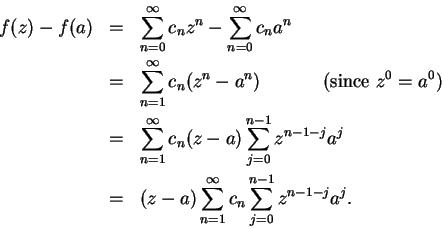
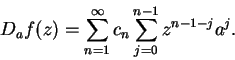
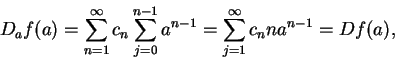
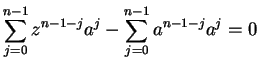 .
.
 . Then
. Then
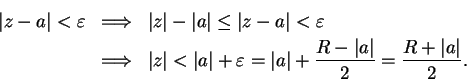
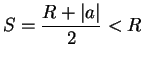 . Then
. Then