



Next: 12.7 Special Values of
Up: 12. Power Series
Previous: 12.5 Logarithms
Index
12.6 Trigonometric Functions
Next we calculate 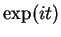 for
for
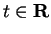 .
.
Now
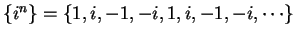 and it is clear that
and it is clear that
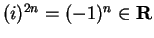 ,
,
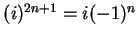 is pure imaginary. Hence,
is pure imaginary. Hence,
i.e.,
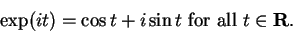 |
(12.46) |
For any complex number 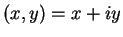 , we have
, we have
Since your calculator has buttons that calculate approximations to  ,
, 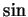 and
and 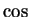 , you can approximately calculate the exponential of any complex number
with a few key strokes.
, you can approximately calculate the exponential of any complex number
with a few key strokes.
The relation (12.46)
actually holds for all
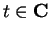 , since
, since
Hence
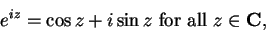 |
(12.47) |
so
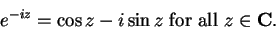 |
(12.48) |
We can solve (12.47) and (12.48) for 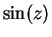 and
and 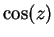 to obtain
to obtain
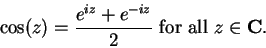 |
(12.49) |
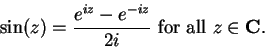 |
(12.50) |
From (12.47) it follows that
i.e., 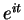 is in the unit circle for all
is in the unit circle for all
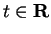 .
.
12.51
Exercise (Addition laws for 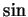 and
and 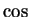 .)
A
.)
A
Prove that
for all
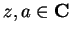
.
By the addition laws, we have (for all
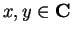 ),
),
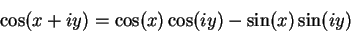 |
(12.52) |
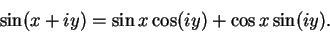 |
(12.53) |
By (12.49) and (12.50)
and
12.54
Definition (Hyperbolic functions.)
For all
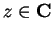
, we define the
hyperbolic sine and
hyperbolic cosine of
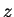
by
Note that if 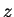 is real,
is real, 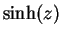 and
and 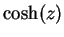 are real. Most calculators have
buttons that calculate
are real. Most calculators have
buttons that calculate 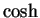 and
and 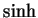 . We can now rewrite (12.52) and
(12.53) as
. We can now rewrite (12.52) and
(12.53) as
These formulas hold true for all complex 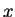 and
and 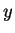 .
.
Since
it follows from our
discussion in example 10.45 that
for all 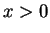 . In particular
. In particular
and
Hence 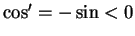 on
on 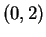 , so
, so 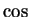 is strictly decreasing on
is strictly decreasing on ![$[0,2]$](img1938.gif) .
Moreover
.
Moreover 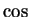 is continuous (since it is differentiable) so by the intermediate
value theorem there is a number
is continuous (since it is differentiable) so by the intermediate
value theorem there is a number 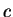 in
in 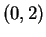 such that
such that 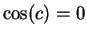 . Since
. Since 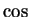 is strictly decreasing on
is strictly decreasing on 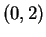 this number
this number 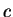 is unique. (Cf. exercise
5.48.)
is unique. (Cf. exercise
5.48.)
12.55
Definition (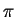 .)
.)
We define the real number
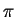
by the condition
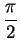
is the unique
number in
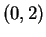
satisfying
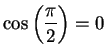
.
12.56
Theorem.
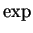 is periodic of period
is periodic of period 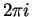 ; i.e.,
; i.e.,
Proof: Since
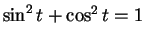 for all
for all
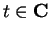 , we have
, we have
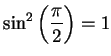 , so
, so
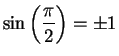 . We have noted that
. We have noted that
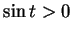 on
on 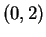 so
so
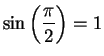 . Hence
. Hence
and
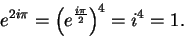 |
(12.57) |
It follows that
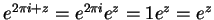 for all
for all
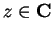 .
.

12.58
Entertainment.
If Maple or Mathematica are asked for the numerical values of
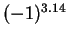
and
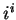
, they agree that
and
Can you propose a reasonable definition for
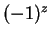
and
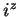
when
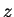
is an
arbitrary complex number, that is consistent with these results? To be reasonable
you would require that when
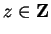
,
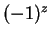
and
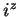
give the expected values,
and
Proof: From the previous exercise,
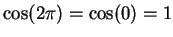 . We've noted that
. We've noted that 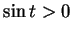 for
for
![${t\in \left(0,{\pi\over 2}\right]}$](img1977.gif) ,
,
Hence 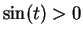 for
for 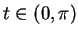 . Hence
. Hence
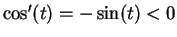 for
for
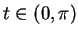 . Hence
. Hence 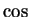 is strictly decreasing on
is strictly decreasing on 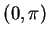 . Hence
. Hence
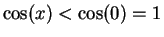 for all
for all 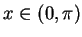 .
.
Now
and since
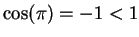 , we've shown that
, we've shown that 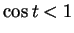 for all
for all 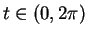 .
.

12.61
Theorem.
Every point 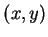 in the unit
circle can be written as
in the unit
circle can be written as
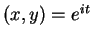 for a unique
for a unique 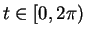 .
.
Proof: We first show uniqueness.
Suppose
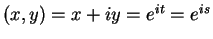 where
where
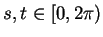 . Without loss of
generality, say
. Without loss of
generality, say 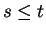 . Then
. Then
and
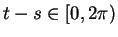 . By the previous theorem,
. By the previous theorem, 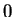 is the only number in
is the only number in
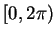 whose cosine is
whose cosine is 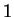 , so
, so 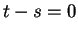 , and hence
, and hence 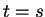 .
.
Let 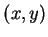 be a point in the unit circle, so
be a point in the unit circle, so 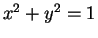 , and hence
, and hence
 . Since
. Since 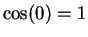 and
and 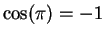 , it follows from the intermediate value
theorem that
, it follows from the intermediate value
theorem that 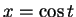 for some
for some ![$t\in[0,\pi]$](img2003.gif) . Then
. Then
so 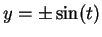 .
.
and since ![$t\in[0,\pi]$](img2003.gif) , we have
, we have
![$2\pi-t\in[\pi,2\pi]$](img2007.gif) .
.

12.62
Lemma.
The set of all complex solutions
to 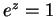 is
is
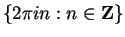 .
.
Proof: By exercise 12.59A
so
Let 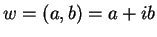 be any solution to
be any solution to 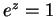 ; i.e.,
; i.e.,
By uniqueness of polar decomposition,
so 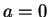 (since for real
(since for real  ,
, 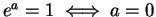 ). We can write
). We can write
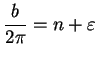 where
where
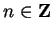 and
and
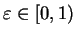 by theorem
5.30 ,
so
by theorem
5.30 ,
so
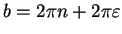 where
where
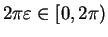 . Now
. Now
By theorem 12.61,
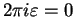 , so
, so 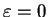 , and
, and 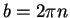 ;
i.e.,
;
i.e., 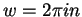 .
.

12.63
Definition (Argument.)
Let
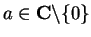
and write

in its polar decomposition
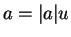
,
where
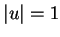
. We know
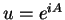
for a unique
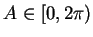
. I will call
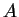
the
argument of

and write
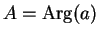
. Hence
12.64
Remark.
Our definition of
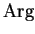
is rather arbitrary. Other natural definitions are
or
None of these argument functions is continuous; e.g.,
But
Proof: Since
the numbers given are solutions to 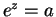 . Let
. Let 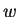 be any solution to
be any solution to 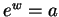 .
Then
.
Then
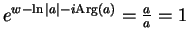 . Hence, by the lemma 12.62,
. Hence, by the lemma 12.62,
We will now look at  geometrically as a function from
geometrically as a function from
 to
to
 .
.
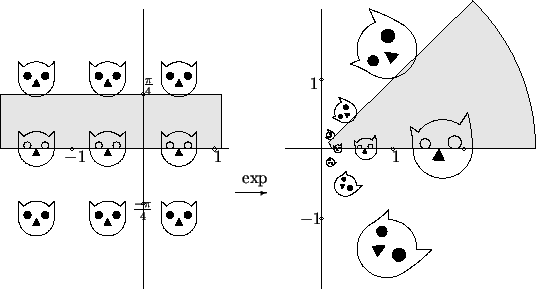
Claim:  maps the vertical line
maps the vertical line 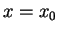 into the circle
into the circle 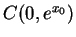 .
.
Proof: If 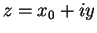 , then
, then
Claim:  maps the horizontal line
maps the horizontal line 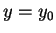 into the ray through
into the ray through 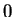 with
direction
with
direction 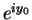 .
.
Proof: If 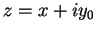 , then
, then
Since 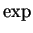 is periodic of period
is periodic of period 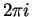 ,
, 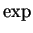 maps an infinite horizontal
strip of width
maps an infinite horizontal
strip of width 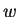 into an infinite circular segment making `` angle
into an infinite circular segment making `` angle 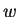 " at the
origin.
" at the
origin.
The Exponentials of Some Cats
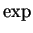 maps every strip
maps every strip
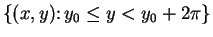 onto all of
onto all of
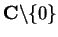 .
.
Proof: These numbers are clearly solutions to 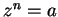 . Let
. Let
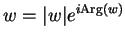 be
any solution to
be
any solution to 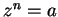 . Then
. Then
By uniqueness of polar decomposition,
i.e., 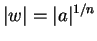 and
and
![$e^{i[n{\mathrm{\rm Arg}}(w)-{\mathrm{\rm Arg}}(a)]}=1$](img2058.gif) . Hence,
. Hence,
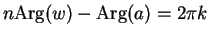 for some
for some
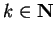 and
and
Thus
For each
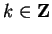 , the number
, the number
is a solution to 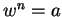 . For
. For 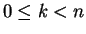 , the numbers
, the numbers
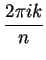 are distinct numbers in
are distinct numbers in 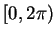 , so the numbers
, so the numbers
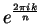 are
distinct. For every
are
distinct. For every
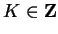 ,
,
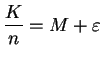 where
where
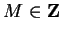 and
and
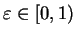 , so
, so
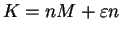 where
where
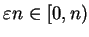 and
and
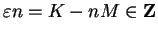 ; i.e.,
; i.e.,
Then
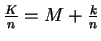 , so
, so




Next: 12.7 Special Values of
Up: 12. Power Series
Previous: 12.5 Logarithms
Index
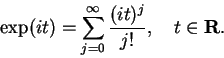
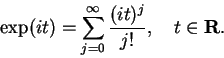
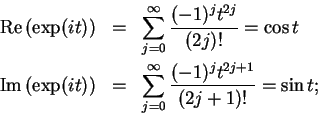
![\begin{eqnarray*}
\exp(x+iy)&=&\exp(x)\exp(iy)=\exp(x)[\cos (y)+i\sin (y)] \\
&=&\exp(x)\cos (y)+i\exp(x)\sin (y).
\end{eqnarray*}](img1906.gif)
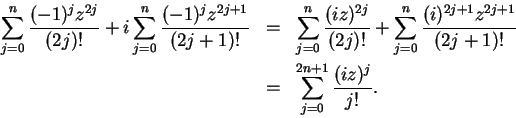
![]() ),
),
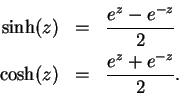
![]() is real,
is real, ![]() and
and ![]() are real. Most calculators have
buttons that calculate
are real. Most calculators have
buttons that calculate ![]() and
and ![]() . We can now rewrite (12.52) and
(12.53) as
. We can now rewrite (12.52) and
(12.53) as
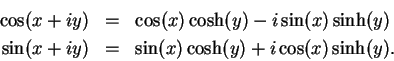
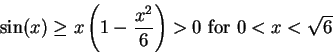
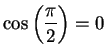 .
.
![]() for all
for all
![]() , we have
, we have
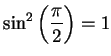 , so
, so
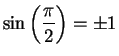 . We have noted that
. We have noted that
![]() on
on ![]() so
so
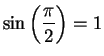 . Hence
. Hence
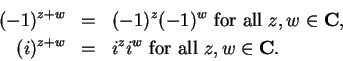
![]() . We've noted that
. We've noted that ![]() for
for
![]() ,
,
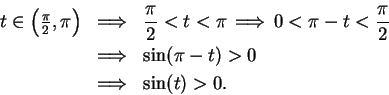
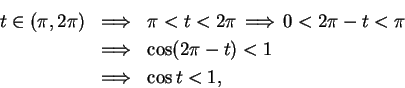
![]() where
where
![]() . Without loss of
generality, say
. Without loss of
generality, say ![]() . Then
. Then
![]() be a point in the unit circle, so
be a point in the unit circle, so ![]() , and hence
, and hence
![]() . Since
. Since ![]() and
and ![]() , it follows from the intermediate value
theorem that
, it follows from the intermediate value
theorem that ![]() for some
for some ![]() . Then
. Then
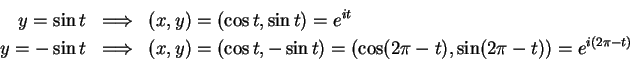
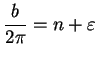 where
where
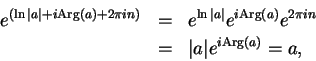
![]() geometrically as a function from
geometrically as a function from
![]() to
to
![]() .
.
![]() maps the vertical line
maps the vertical line ![]() into the circle
into the circle ![]() .
.
![]() , then
, then
![]() maps the horizontal line
maps the horizontal line ![]() into the ray through
into the ray through ![]() with
direction
with
direction ![]() .
.
![]() , then
, then
![]() maps every strip
maps every strip
![]() onto all of
onto all of
![]() .
.
![]() . Let
. Let
![]() be
any solution to
be
any solution to ![]() . Then
. Then
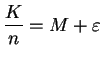 where
where