



Next: 6. The Complex Numbers
Up: 5. Real Numbers
Previous: 5.2 Completeness
Index
5.35
Definition (Graph.)
Let
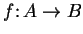
be a function. The
graph of 
is
5.36
Remark.
If

is a function from

to

, then graph

is
You may find it useful to think of

as points on a line, and
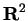
as points in a plane and to represent the graph by a picture. Any such picture is
outside the scope of our formal development, but I will draw lots of such pictures
informally.
5.37
Definition (Sum and product of functions.)
Let

be a field, and let
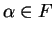
. Let
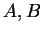
be sets and let
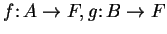
be functions. We define functions
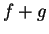
,
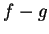
,
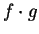
,
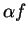
and
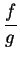
by:
where
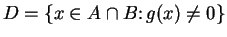
.
5.38
Remark.
Let

be a field, let

be a set, and let
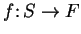
,
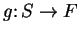
be functions with the same domain. Then the operations
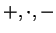
are binary operations on the set
of all functions from

to

. These
operations satisfy the same commutative, associative and distributive laws that the
corresponding operations on

satisfy; e.g.,
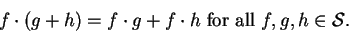 |
(5.39) |
Proof of (5.39). For all 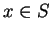 ,
,
Hence,
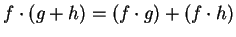
. (Two functions are equal when they have
the same domain, the same codomain, and the same rule.)

5.42
Exercise.
Is there a function
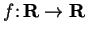
that is both increasing and decreasing?
If the answer is yes, give an example. If the answer is no, explain why not.
5.43
Exercise.
Give an example of a function
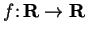
such that

is increasing,
but not strictly increasing.
5.44
Exercise.
Let
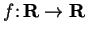
and
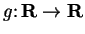
be increasing functions. Either
prove that
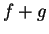
is increasing or give an example to show that
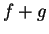
is not
necessarily increasing
5.45
Exercise.
Let
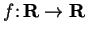
and
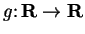
be increasing functions. Either
prove that
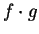
is increasing or give an example to show that
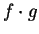
is not
necessarily increasing.
5.46
Theorem.
Let
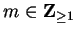 , let
, let
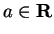 ,
, 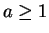 . Then
. Then 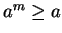 .
.
The proof is by induction, and is omitted.
5.47
Theorem.
Let
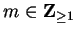 . Let
. Let 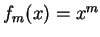 for all
for all
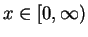 in
in
 . Then
. Then
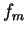 is strictly increasing on
is strictly increasing on 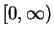 .
.
Proof: The proof follows from induction on 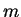 or by factoring
or by factoring 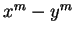 ,
and is omitted.
,
and is omitted.
5.48
Exercise.
A
Let
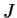
be an interval
in

and let
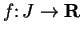
be a
strictly increasing function on
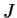
. Show that for each
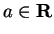
the equation
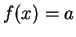
has at most one solution

in
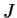
.
Proof: First I will construct a binary search sequence ![$\{[a_n,b_n]\}$](img1289.gif) in
in
 such
that
such
that
By completeness of
 , I'll have
, I'll have
![$\{[a_n,b_n]\}\to c$](img1439.gif) for some
for some
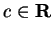 . I'll
show
. I'll
show 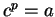 , and the proof will be complete.
, and the proof will be complete.
Let
![$[a_0,b_0]=[0,(1+a)]$](img1442.gif) . Then
. Then
For
 , define
, define
The proof that ![$\{[a_n,b_n]\}$](img1289.gif) is a binary search sequence and that
is a binary search sequence and that
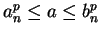 for all
for all
 is the same as the proof given in example 5.16 for
is the same as the proof given in example 5.16 for
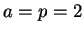 , and will not be repeated here. By completeness
, and will not be repeated here. By completeness
![$\{[a_n,b_n]\}\to c$](img1439.gif) for
some
for
some
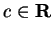 . Since
. Since
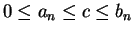 , we have
, we have
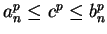 .
It follows that
.
It follows that
By the formula for factoring 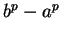 (cf. (3.78)), we have
(cf. (3.78)), we have
for all
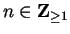 . By Archimedean property 3
(cf corollary 5.28),
it follows that
. By Archimedean property 3
(cf corollary 5.28),
it follows that 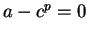 , i.e
, i.e 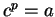 .
.
Let 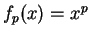 . Since
. Since 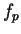 is
strictly increasing on
is
strictly increasing on
 , it follows from exercise 5.48A that
, it follows from exercise 5.48A that 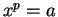 has
at most one solution in
has
at most one solution in
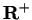 and this completes the proof of the theorem.
and this completes the proof of the theorem.

5.50
Notation (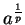 .)
.)
If
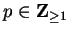
and
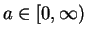
, then the unique number
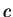
in
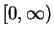
such that
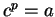
is denoted by
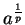
,
and is called the
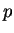 th root of
th root of 
.
An alternative notation for
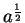
is
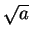
.
5.51
Exercise.
A
Let
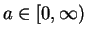
, let
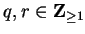
, and
let
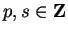
.
- a)
- Show that
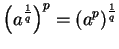 .
.
- b)
- Show that if
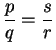 , then
, then
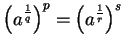 .
.
5.52
Definition (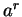 .)
.)
If
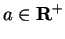
and
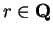
we define
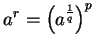
where
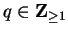
,
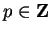
and
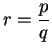
. The previous exercise shows
that this definition does not depend on what representation we use for writing
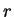
.
5.53
Theorem (Laws of exponents.),
For all
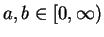 and all
and all
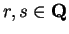
- a)
-
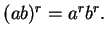
- b)
-
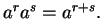
- c)
-
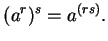
Proof: [of part b)]
Let
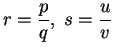 where
where 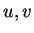 are integers and
are integers and 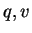 are
positive integers. Then (by laws of exponents for integer exponents),
are
positive integers. Then (by laws of exponents for integer exponents),
Also,
Hence,
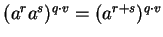 , and hence
, and hence
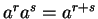 by
uniqueness of
by
uniqueness of 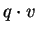 roots.
roots.
5.54
Exercise.
A
Prove parts a) and c) of theorem
5.53.
5.55
Entertainment.
Show that of the two real numbers
one is in
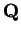
, and the other is not in
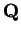
.
5.56
Note.
The Archimedean property was stated by Archimedes
in the following form:
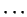 the following lemma is assumed: that the excess by which
the greater of (two) unequal areas exceeds the less can,
by being added to itself, be made to exceed any given finite area.
The earlier geometers have also used this lemma.[2, p 234]
the following lemma is assumed: that the excess by which
the greater of (two) unequal areas exceeds the less can,
by being added to itself, be made to exceed any given finite area.
The earlier geometers have also used this lemma.[2, p 234]
Euclid indicated that his arguments needed the Archimedean
property by using the following definition:
Magnitudes are said to have a ratio to one another which are
capable, when multiplied, of exceeding one another.[19, vol 2, p114]
Here ``multiplied'' means ``added to itself some number of times'', i.e.
``multiplied by some positive integer''.
Rational exponents were introduced by Newton
in 1676.
Since algebraists write 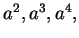 etc., for
etc., for 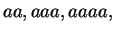 etc.,
so I write
etc.,
so I write
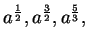 for
for
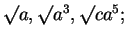 and I write
and I write
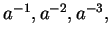 etc.
for
etc.
for
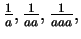 etc.[14, vol 1, p355]
etc.[14, vol 1, p355]
Here
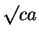
denotes the cube root of

.
Buck's Advanced Calculus[12, appendix 2] gives eight
different characterizations of the completeness axiom
and discusses
the relations between them.
The term completeness is a twentieth century
term. Older books speak about the continuity
of the real numbers to describe what we call completeness.




Next: 6. The Complex Numbers
Up: 5. Real Numbers
Previous: 5.2 Completeness
Index
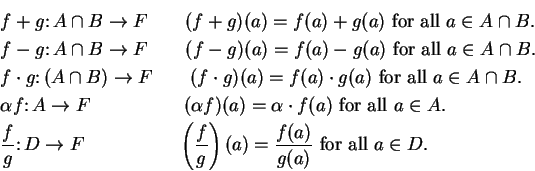
![]() ,
,
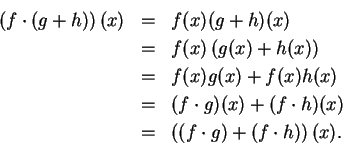
![]() or by factoring
or by factoring ![]() ,
and is omitted.
,
and is omitted.
![]() in
in
![]() such
that
such
that
![]() . Then
. Then
![\begin{displaymath}[a_{n+1},b_{n+1}]=\cases{ \left[a_n,{{a_n+b_n}\over 2}\right]...
...2}, b_n\right] &if $\left( {{a_n+b_n}\over 2}\right)^p
<a$.\cr}\end{displaymath}](img1444.gif)
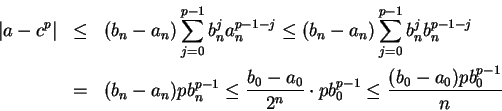
![]() . Since
. Since ![]() is
strictly increasing on
is
strictly increasing on
![]() , it follows from exercise 5.48A that
, it follows from exercise 5.48A that ![]() has
at most one solution in
has
at most one solution in
![]() and this completes the proof of the theorem.
and this completes the proof of the theorem.
![]()
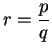 . The previous exercise shows
that this definition does not depend on what representation we use for writing
. The previous exercise shows
that this definition does not depend on what representation we use for writing 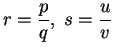 where
where ![]() are integers and
are integers and ![]() are
positive integers. Then (by laws of exponents for integer exponents),
are
positive integers. Then (by laws of exponents for integer exponents),
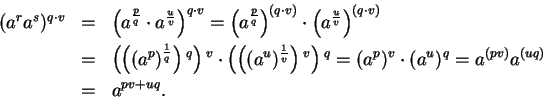
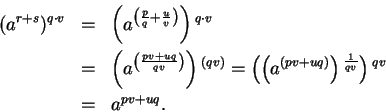
the following lemma is assumed: that the excess by which the greater of (two) unequal areas exceeds the less can, by being added to itself, be made to exceed any given finite area. The earlier geometers have also used this lemma.[2, p 234]
etc., for
etc., so I write
for
and I write
etc. for
etc.[14, vol 1, p355]