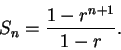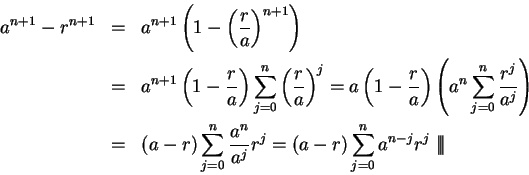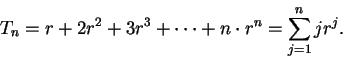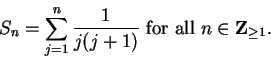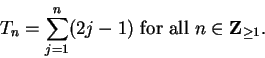Next: 3.5 Maximum Function
Up: 3. Induction and Integers
Previous: 3.3 Recursive Definitions.
Index
3.65
Notation (
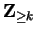 .)
.)
Let
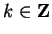
. We define
In
particular
.
3.66
Definition (
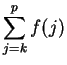 )
)
Let
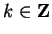
and let
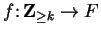
be a function from
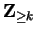
to
a field

. Define a function
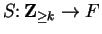
by the rules
Hence, for
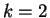
,
We denote
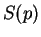
by
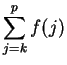
for all
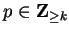
. Thus,
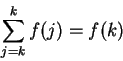 |
(3.67) |
and
The letter
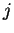
in (
3.67) has no meaning, and can be replaced by any symbol
that has no meaning in the present context. Thus
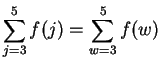
.
3.70
Remark.
Usually induction arguments are presented less formally than I have been presenting
them. In the proof of the next theorem I will give a more typical looking induction
argument. (I personally find the more formal version - where a proposition is
actually named - easier to understand.)
Proof: (By induction.) When 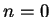 , (3.72) says
, (3.72) says
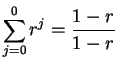 which is true since both sides are equal to
which is true since both sides are equal to
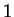 . Now suppose that (3.72) is true for some
. Now suppose that (3.72) is true for some
 . Then
. Then
so
Hence, if (3.72) holds for some
 , it also holds when
, it also holds when  is replaced by
is replaced by
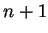 . By induction (3.72) holds for all
. By induction (3.72) holds for all
 .
.

3.73
Remark.
I will sometimes denote
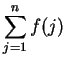
by
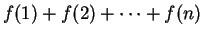
. I am not going to give a formal
definition for
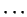
,
and when you see
written
in these notes it is usually an indication that a
straightforward induction argument or a recursive
definition is being omitted.
3.74
Remark.
The previous proof was easy, but in order to use the induction proof, I
needed to know the formula. Here I will indicate how one might discover such
a formula. For each

, let
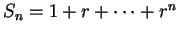
. Then
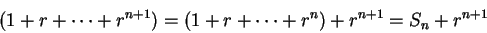 |
(3.75) |
and
Hence
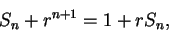 |
(3.76) |
and it follows that
i.e.
Here I have derived the formula (
3.72).
If you write out the argument from line (
3.75)
to line (
3.76), without using
s, and using only
properties of sums that we have explicitly proved or assumed,
you will probably be surprised at how many implicit assumptions
were made above. However all of the assumptions can be justified
in a straightforward way.
Proof: Let
 . The formula (3.72) for a finite geometric series
shows that
. The formula (3.72) for a finite geometric series
shows that
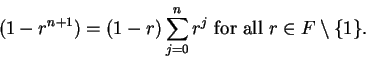 |
(3.79) |
This formula also holds when 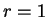 , since then both sides of the equation
are equal to zero, so
, since then both sides of the equation
are equal to zero, so
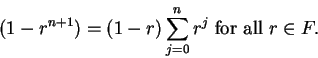 |
(3.80) |
This proves our formula in the case 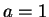 .
When
.
When 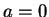 , equation (3.78) says
, equation (3.78) says
which is true, so we will suppose that 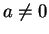 .
Then by (3.80) we have
.
Then by (3.80) we have
3.81
Remark.
The solution to the problem
of ``factoring'' an expression depends on the field over which
we are working. For example, if we work over
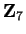
, then
whereas if

is an ordered field, then
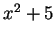
does not factor in the form
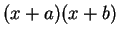
, where

and
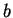
are in

. (If
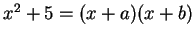
for all
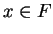
, then by taking
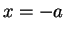
we would get
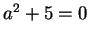
,
which is false since
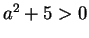
in any ordered field.)
3.83
Entertainment.
Let

be a field and let
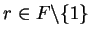
. For all
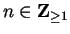
, let
By looking at
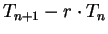
and using the known formula (
3.72),
derive the formula
3.84
Exercise.
A
Let
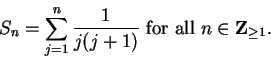 |
(3.85) |
Calculate the values for
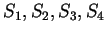
. Write your answers as fractions in the
simplest form you can. Then guess a formula for
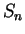
, and prove that it is valid
for all
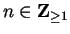
.
3.86
Exercise.
A
Let
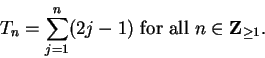 |
(3.87) |
Calculate the values for
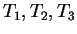
, and
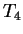
. Then guess a formula for
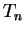
,
and prove that your guess is correct.




Next: 3.5 Maximum Function
Up: 3. Induction and Integers
Previous: 3.3 Recursive Definitions.
Index
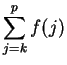 )
Let
)
Let
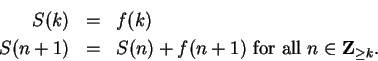
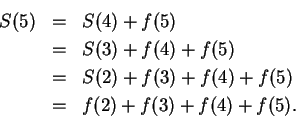
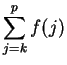 for all
for all
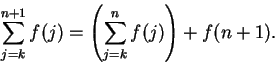
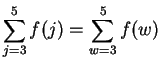 .
.
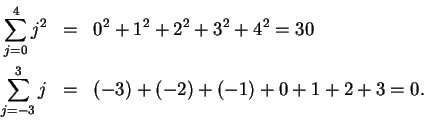
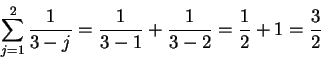
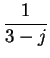 is not defined for all
is not defined for all
![]() be functions from
be functions from
![]() to an ordered field
to an ordered field ![]() , and let
, and let
![]() . Then
. Then
![$\displaystyle {\sum_{j=k}^p f(j)+\sum_{j=k}^p g(j)=\sum_{j=k}^p [f(j)+g(j)]\mbox{ for all }
p\in\mbox{{\bf Z}}_{\geq k}.}$](img1038.gif)
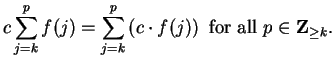
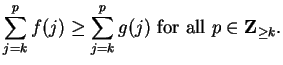
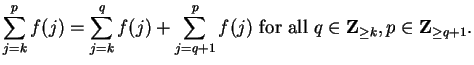
![]() , (3.72) says
, (3.72) says
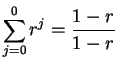 which is true since both sides are equal to
which is true since both sides are equal to
![]() . Now suppose that (3.72) is true for some
. Now suppose that (3.72) is true for some
![]() . Then
. Then
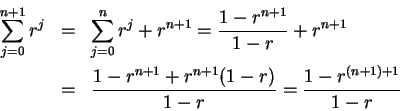
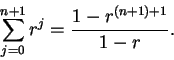
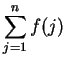 by
by